Predicting Camera Viewpoint Improves Cross-dataset Generalization
for 3D Human Pose Estimation

Monocular estimation of 3d human pose has attracted increased attention with the availability of large ground-truth motion capture datasets. However, the diversity of training data available is limited and it is not clear to what extent methods generalize outside the specific datasets they are trained on. In this work we carry out a systematic study of the diversity and biases present in specific datasets and its effect on cross-dataset generalization across a compendium of 5 pose datasets. We specifically focus on systematic differences in the distribution of camera viewpoints relative to a body-centered coordinate frame. Based on this observation, we propose an auxiliary task of predicting the camera viewpoint in addition to pose. We find that models trained to jointly predict viewpoint and pose systematically show significantly improved cross-dataset generalization. (High Resolution PDF) (Low Resolution PDF) (pre-trained GPA model)

This work was supported in part by NSF grants IIS-1813785, IIS-1618806, and a hardware gift from NVIDIA.

We ask the reader to consider the game of "Name That Dataset" in homage to Torralba et al. Can you guess which dataset each image belongs to? More importantly, if we train a model on the Human3.6M dataset how well would you expect it to perform on each of the images depicted?

Answer key: Metric: MPJPE, the lower the better. 1) GPA: 69.7 mm 2) H36M: 29.2 mm, 3) 3DPW, 71.2 mm, 4) 3DHP 107.7 mm, 5) 3DPW 66.2 mm, 6) SURREAL 83.4 mm, H36M image performs best while 3DHP image performs worst.

Comparison of existing datasets commonly used for training and evaluating 3D human pose estimation methods. We calculate the mean and std of camera distance, camera height, focal length, bone length from training set. Focal length is in mm while the others are in unit meters. 3DHP has two kinds of cameras and the training set provide 28 joints annotation while test set provide 17 joints annotation.

Distribution of camera viewpoints relative to the human subject. We show the distribution of camera azimuth (−180◦ , 180◦) and elevation (−90◦, 90◦) for 50k poses sampled from each representative dataset (H36M, GPA, SURREAL, 3DPW, 3DHP).

Pose space (root-relative vs body-center coordinate) visualized using UMAP[18]. We can see root-relative is a better choice as it is more separable.

Pose space (root-relative vs body-center coordinate) after normalization and visualized using UMAP[18]. We can see root-relative is a better choice as it is more separable.

We treat the different datasets pose as a classsification problem, with the MNIST network we get the classification acc as below to further verify the Root-relative space is better than body-centered coordinates.

First: Illustration of our body-centered coordinate frame (up vector, right vector and front vector) relative to a camera-centered coordinate frame. Second-Sixth: Camera viewpoint distribution of the 5 datasets color by quaternion cluster index. Quaternions (rotation between body-centered and camera frame) are sampled from training sets and clustered using k-means.

Think it too colorful? We remove the color coding for each of the quaternion center, and show the quaternion k-means cluster centers as point as below:

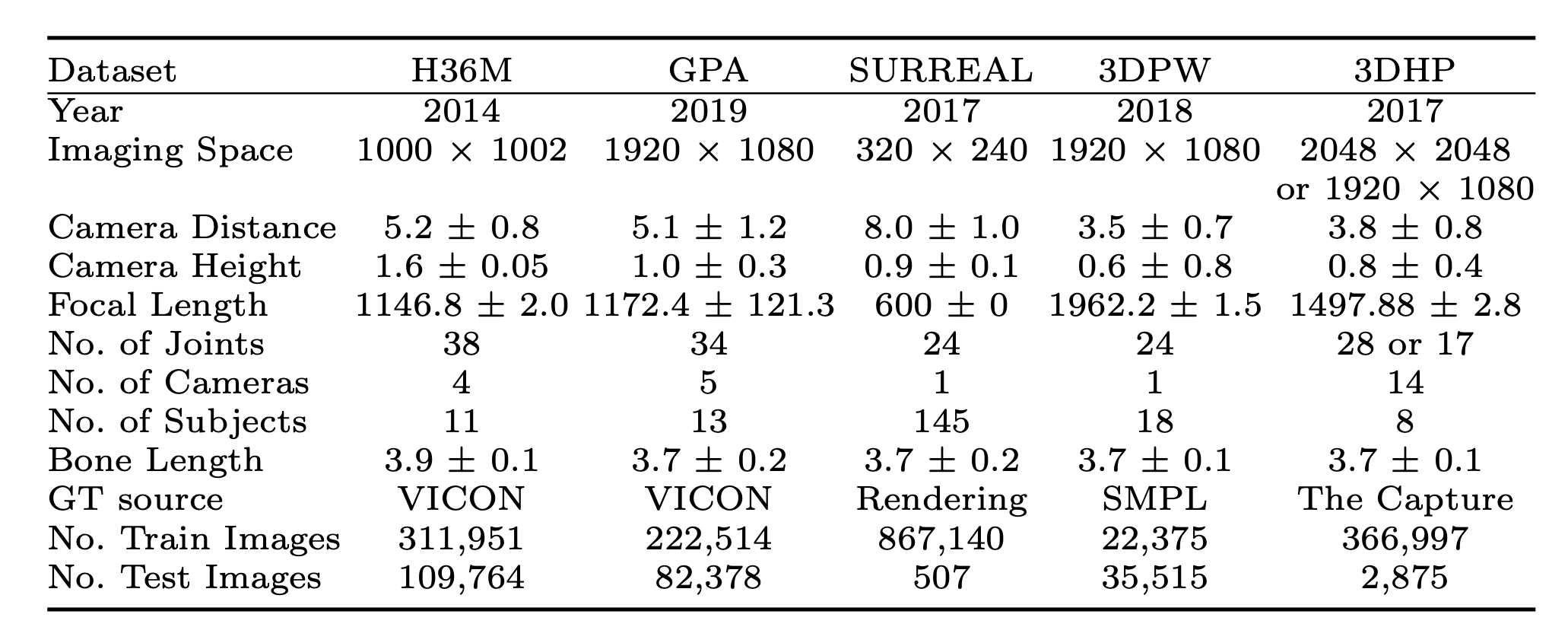
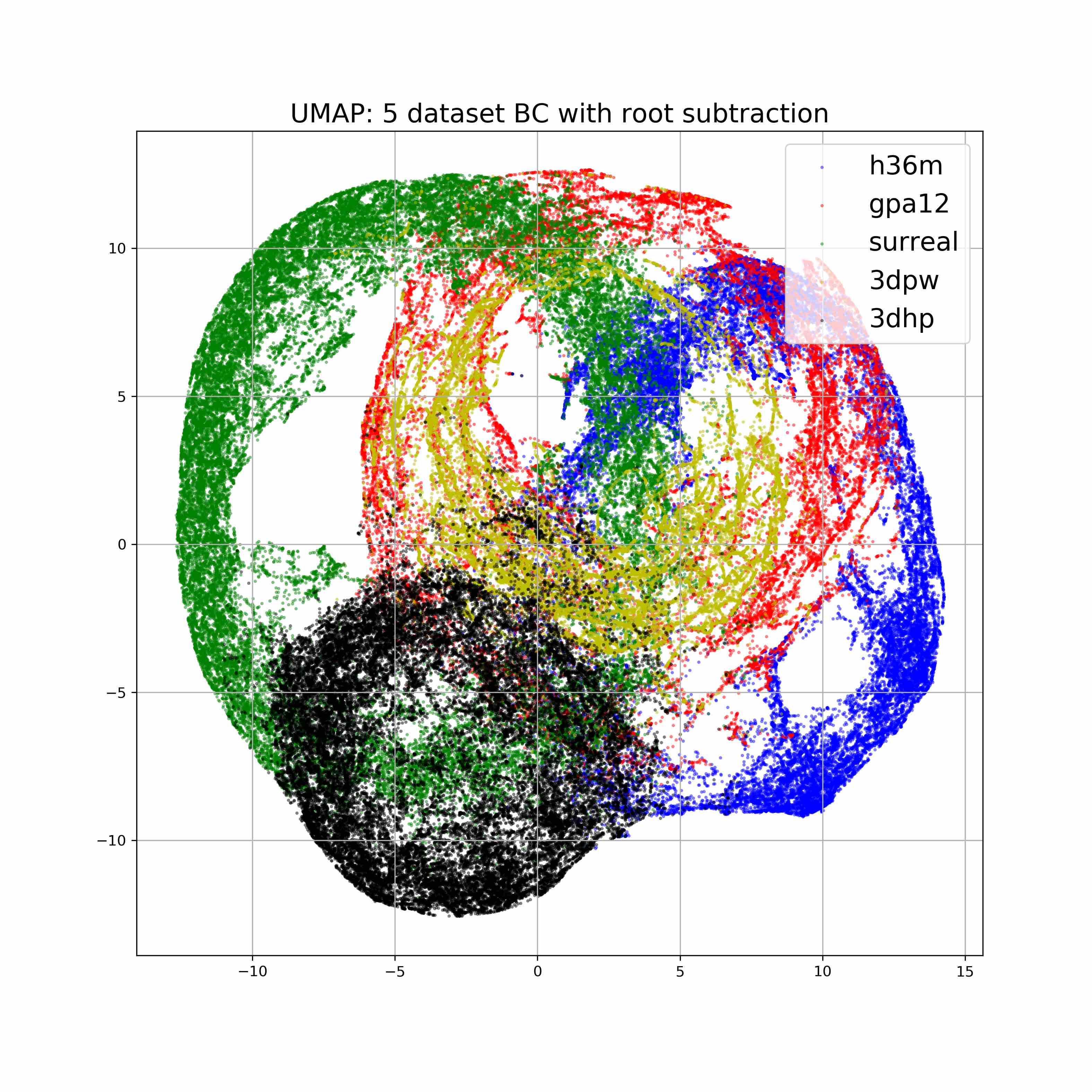
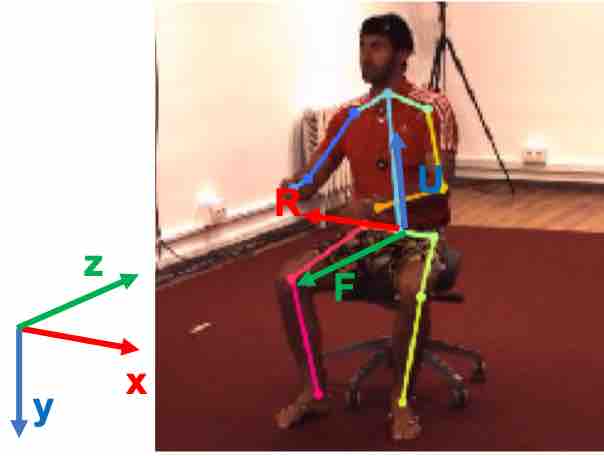
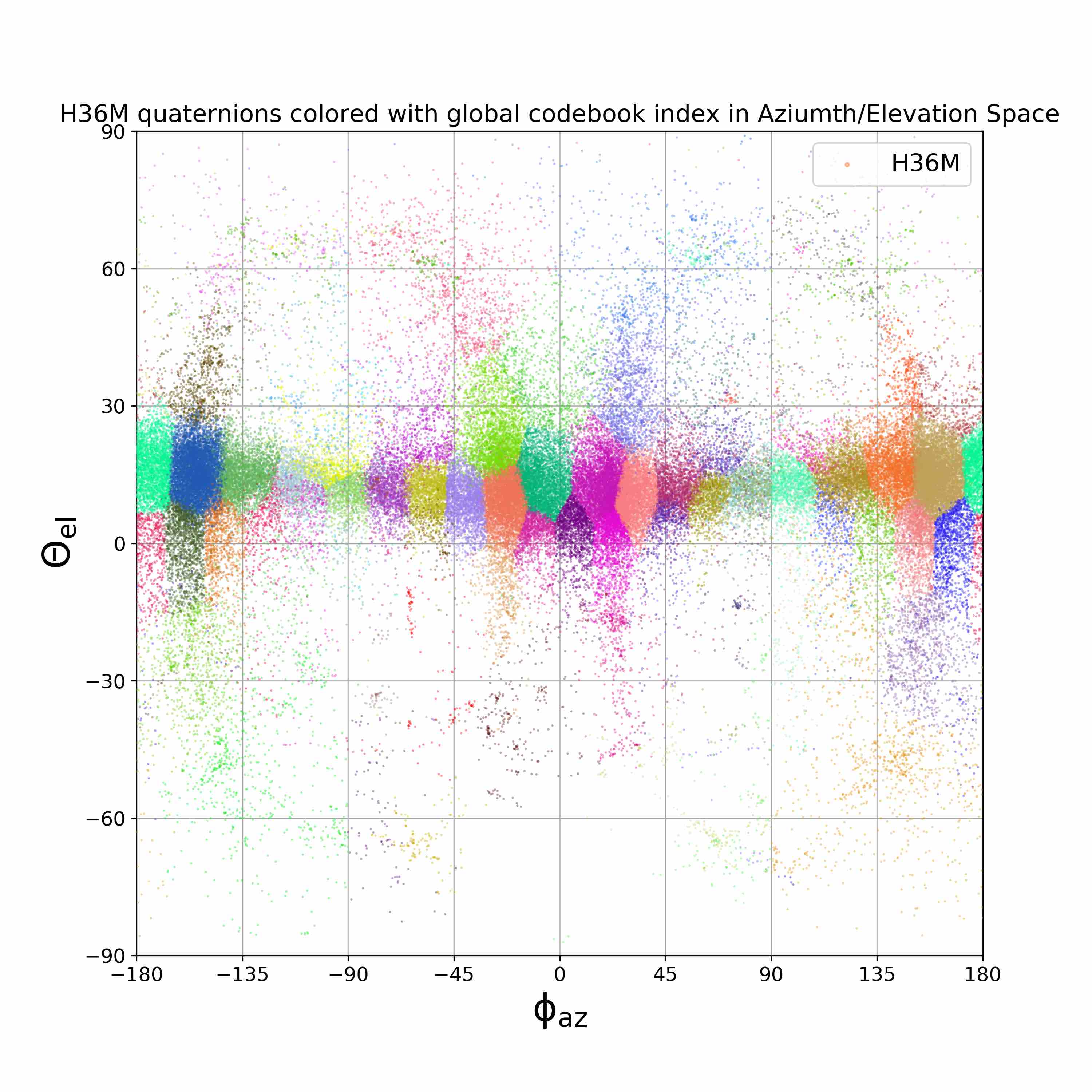
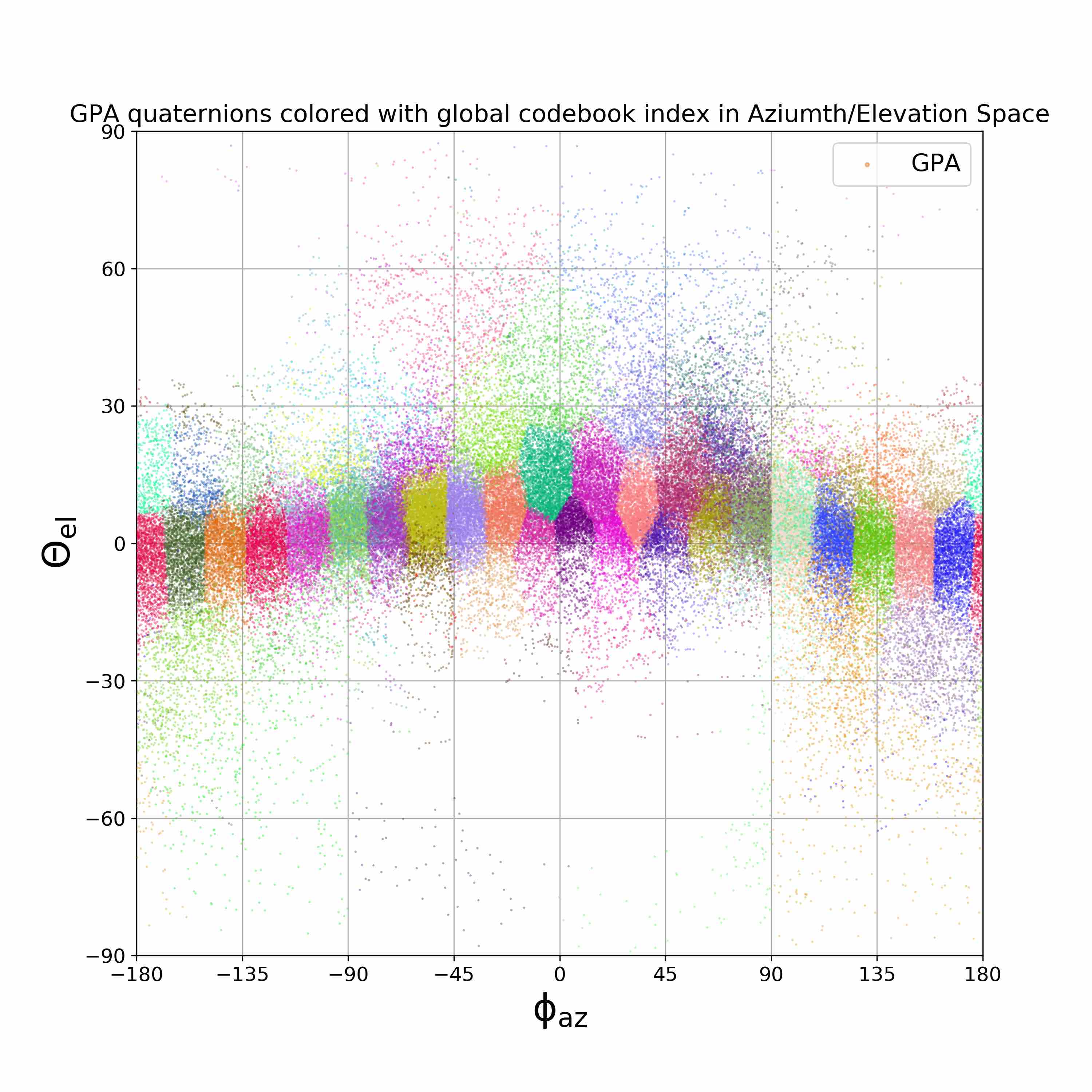
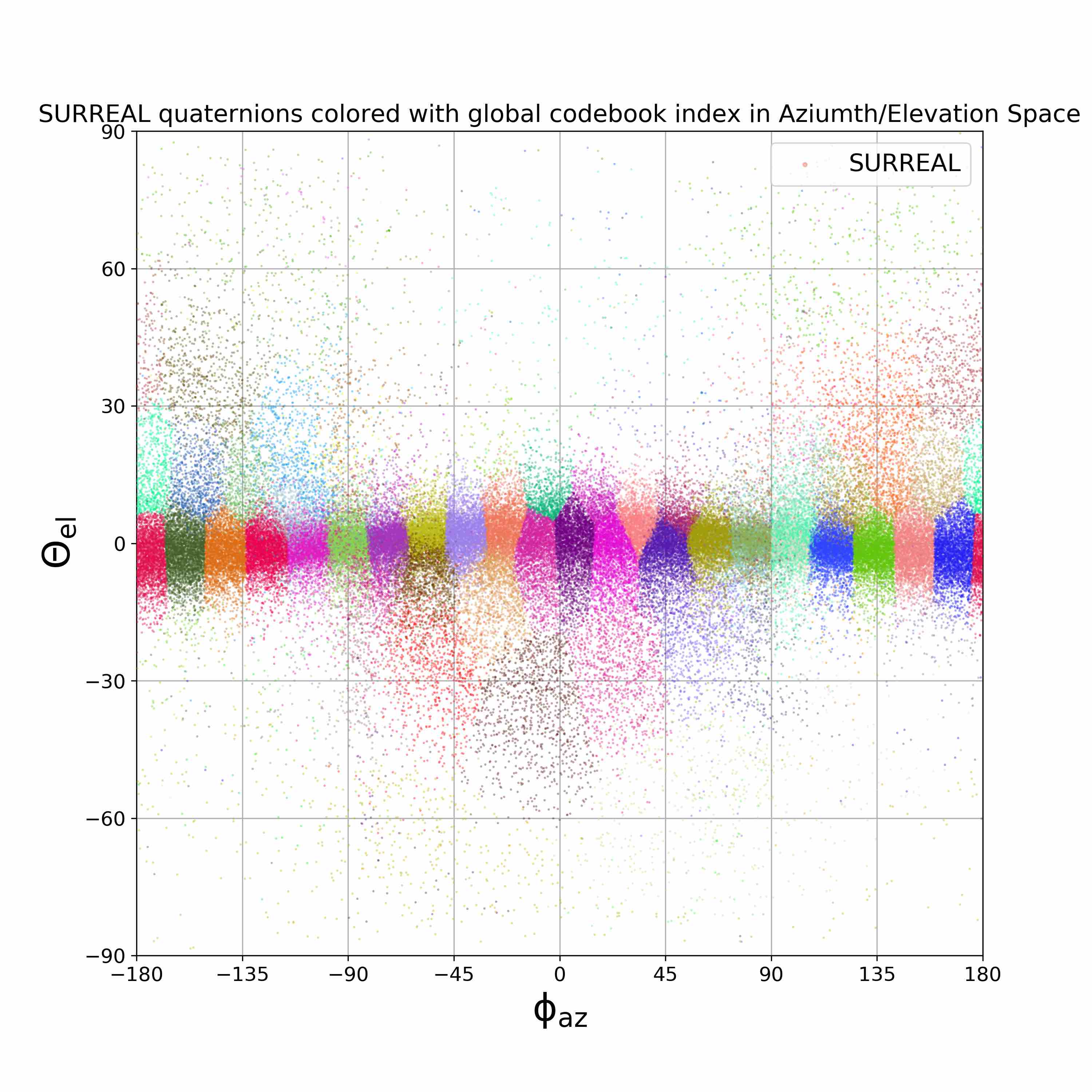
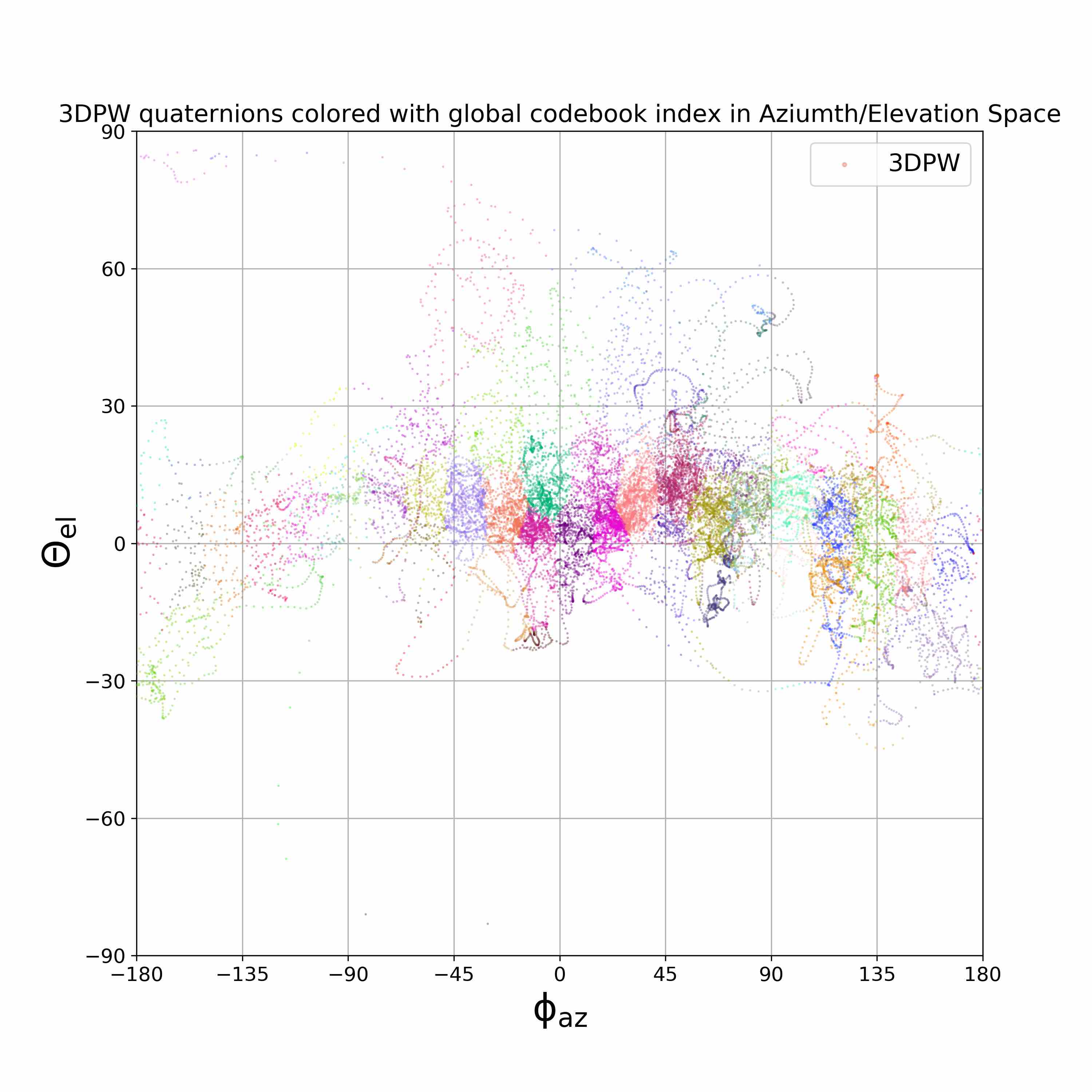
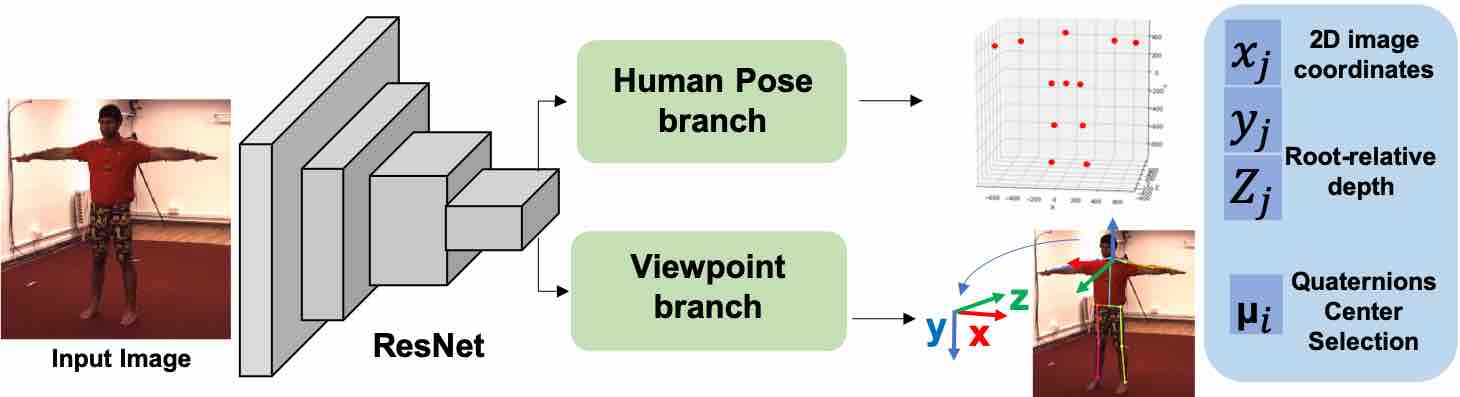
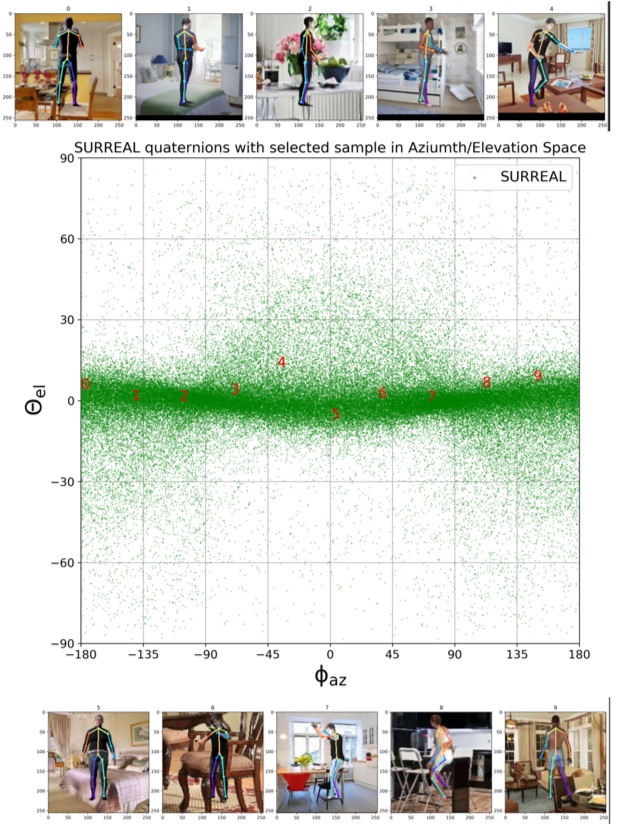
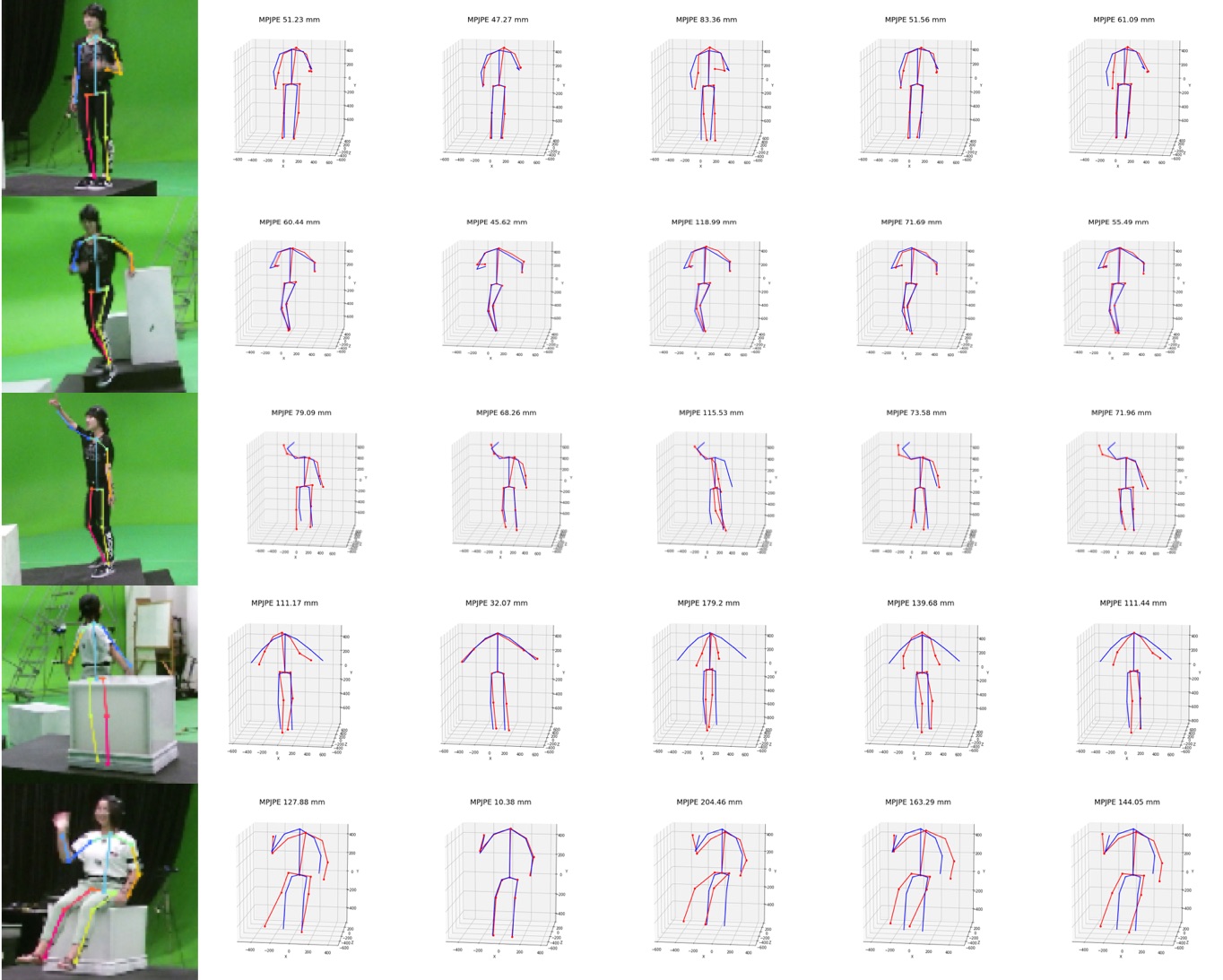
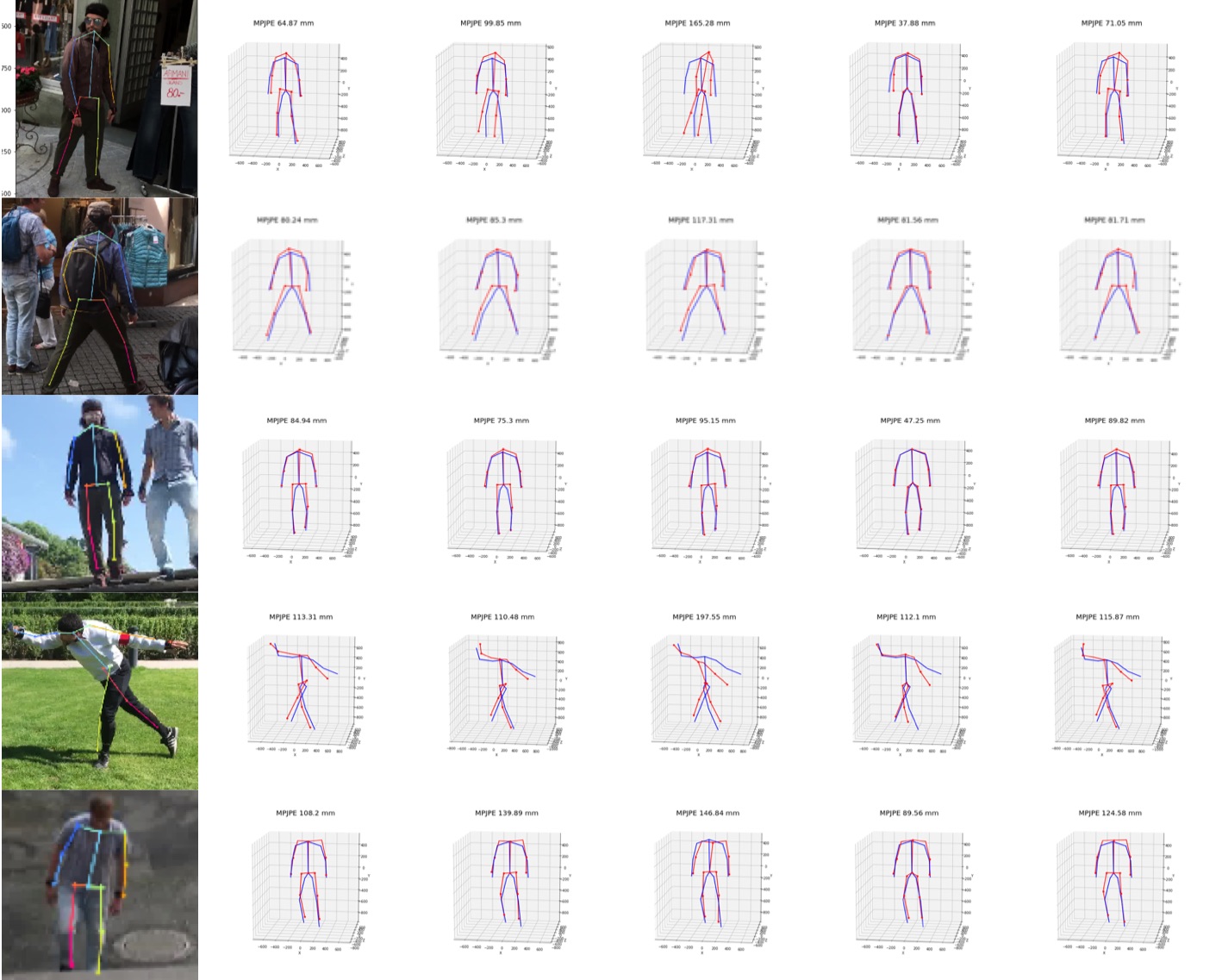
Flowchart of our model. We augment a model which predicts cameracentered 3d pose using the human pose branch with an additional viewpoint branch that selections among a set of quantized camera view directions.
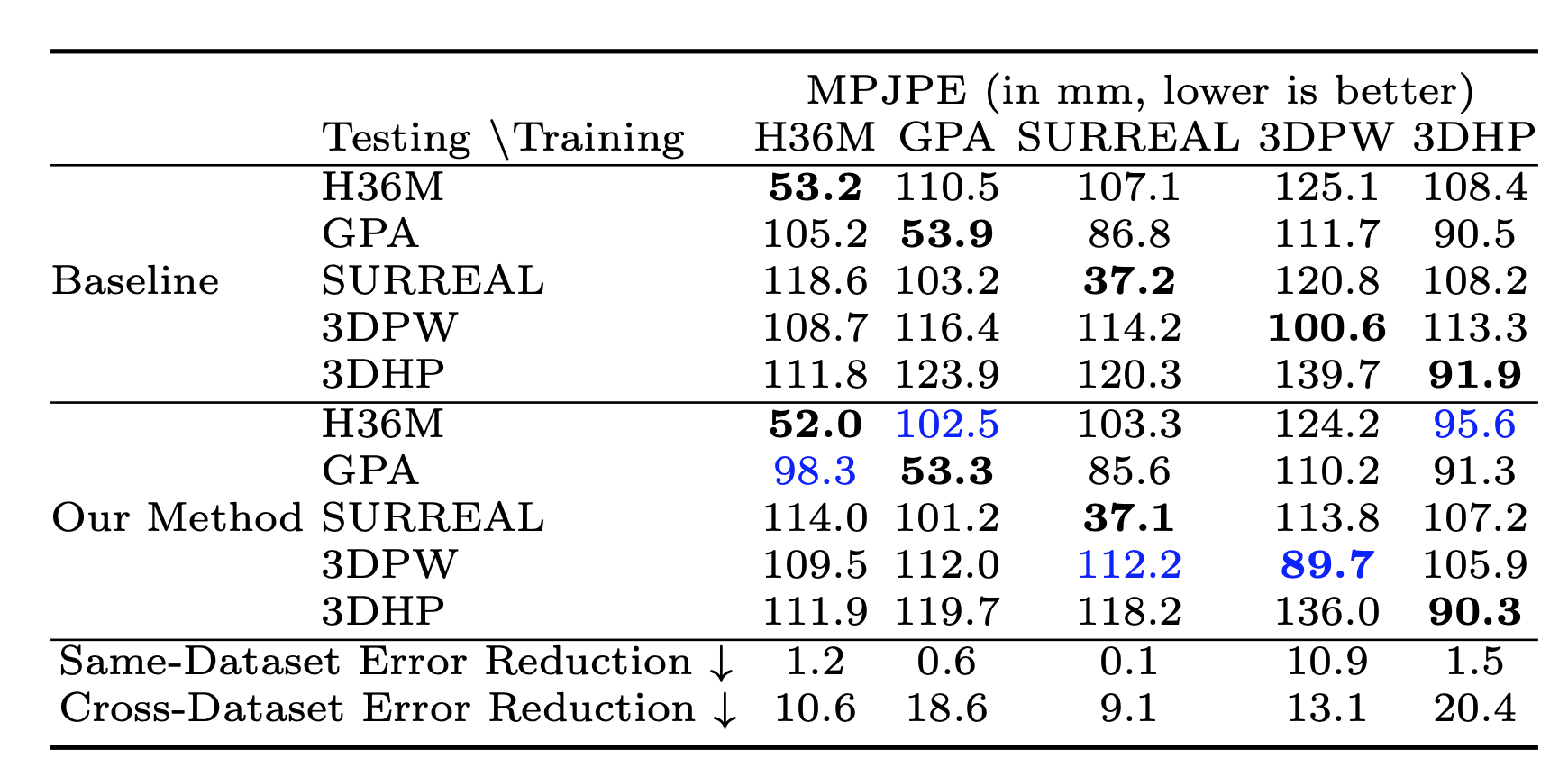
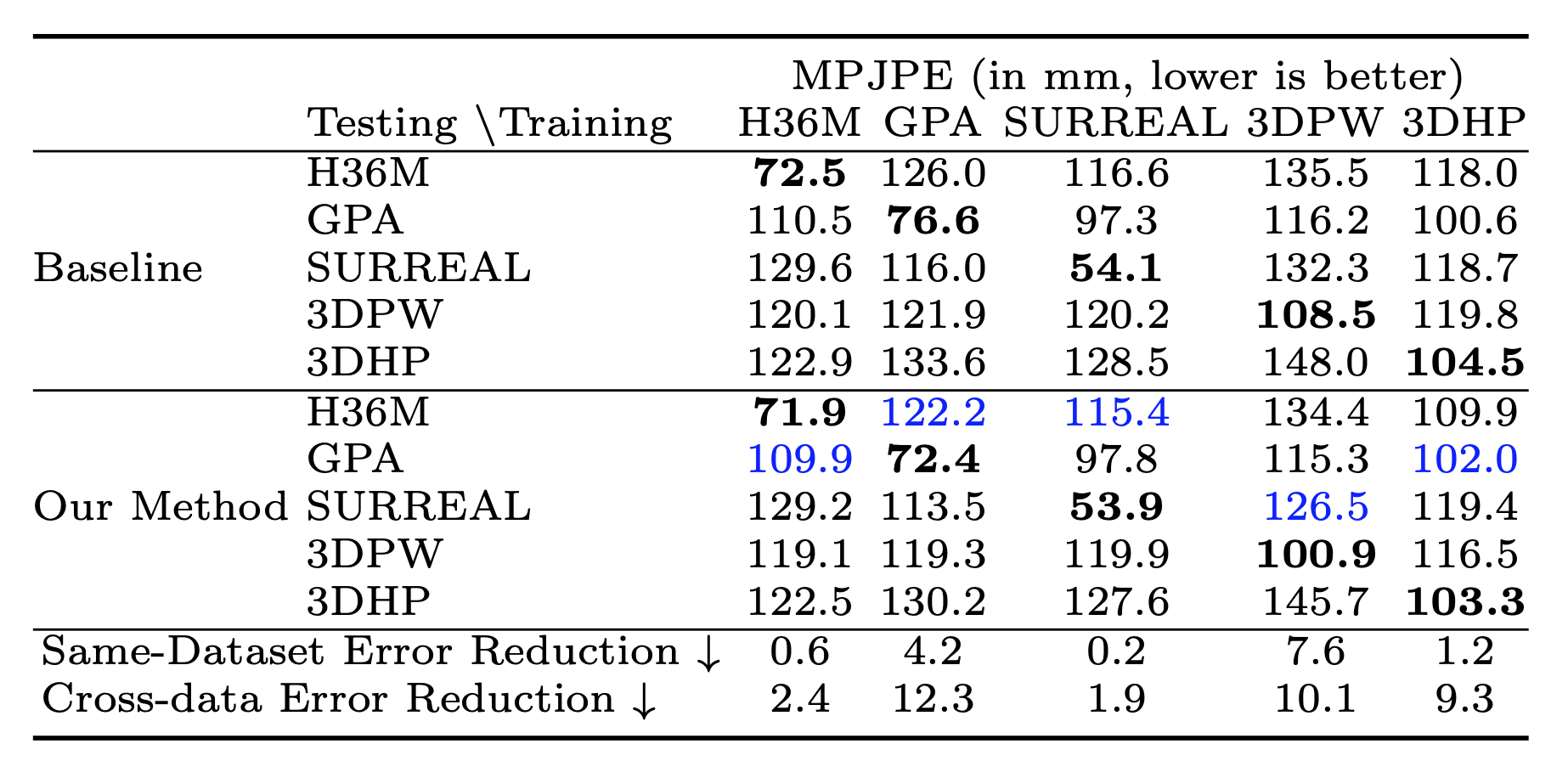
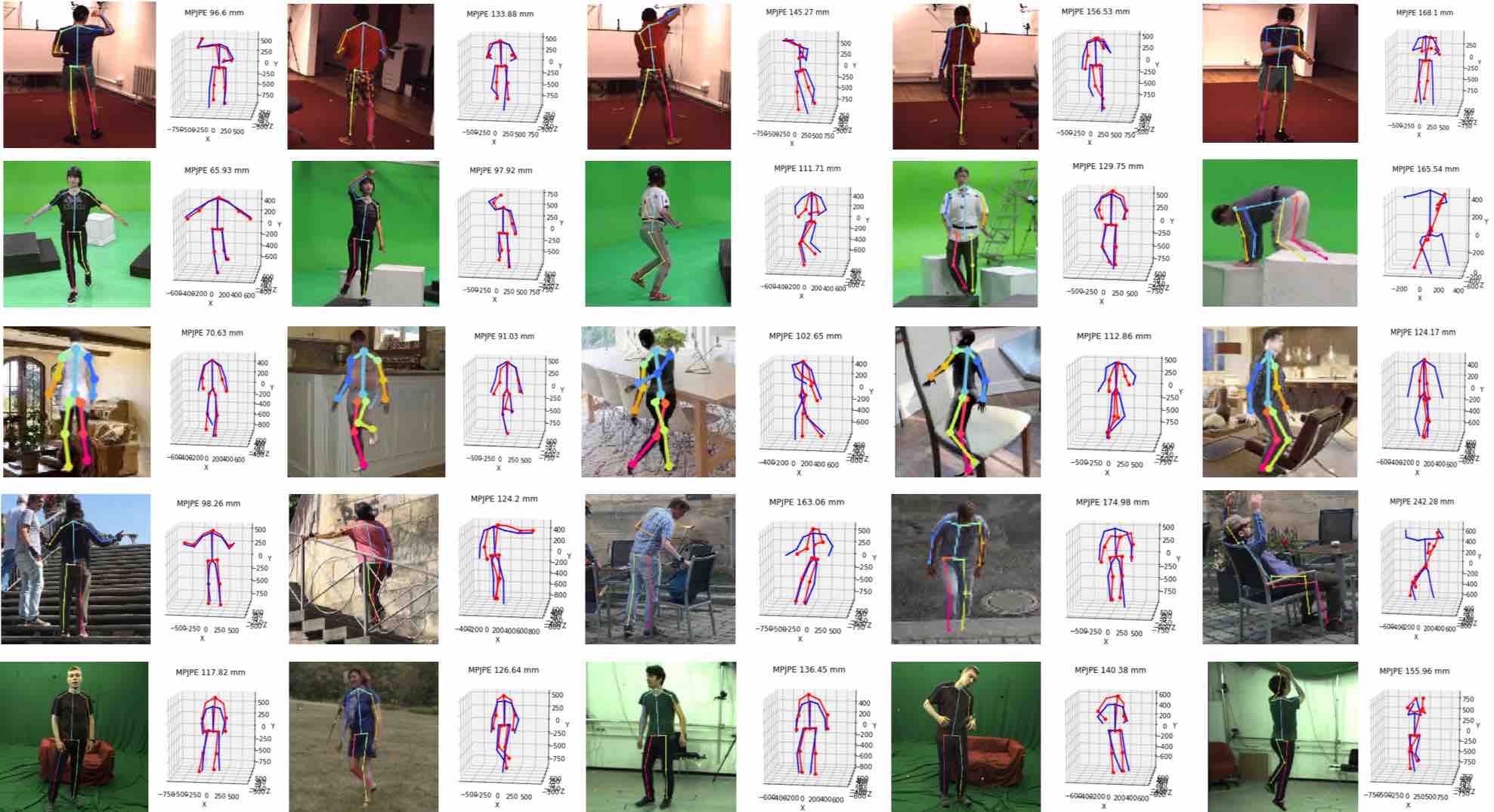
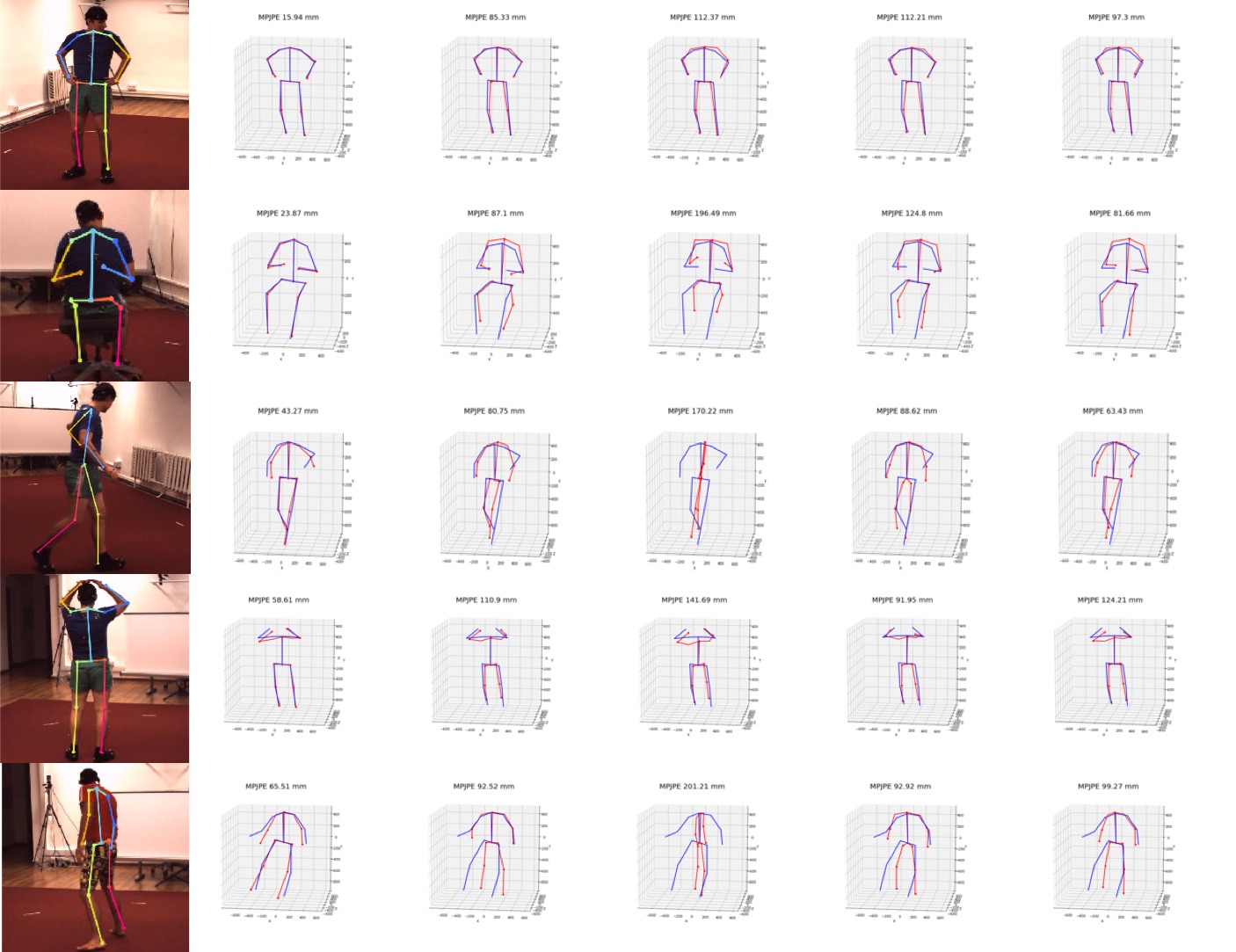
Baseline cross-dataset test error and error reduction from the addition of our proposed quaternion loss. Bold indicates the best performing model on each the test set (rows). Blue color indicates test set which saw greatest error reduction.
Comparison to state-of-the-art performance. There are many missing entries, indicating how infrequent it is to perform multi-dataset evaluation. Our model provides a new state-of-the art baseline across all 5 datasets and can serve as a reference for future work. * denotes training using extra data or annotations (e.g. segmentation). Underline denotes the second best results.
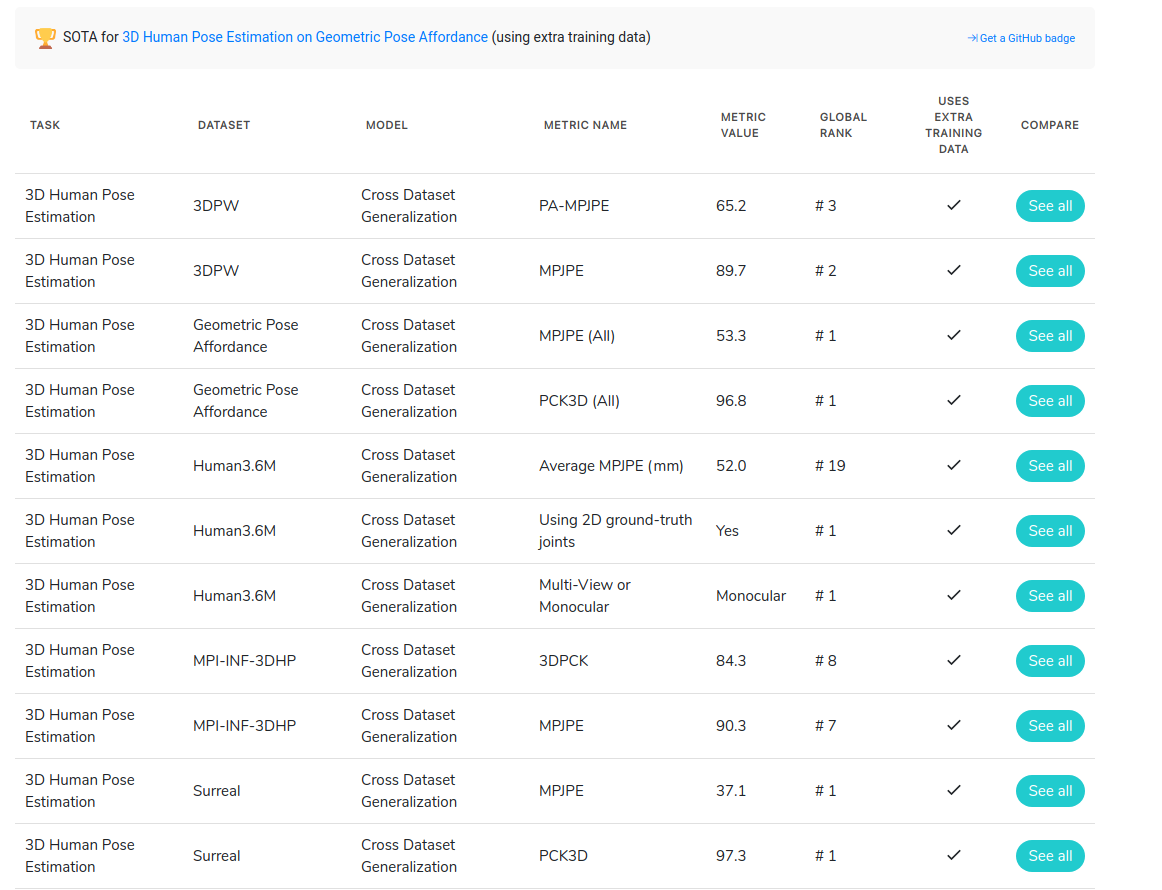
Screenshot of our methods on Paper-with-code webpage on April 12th, 2020.
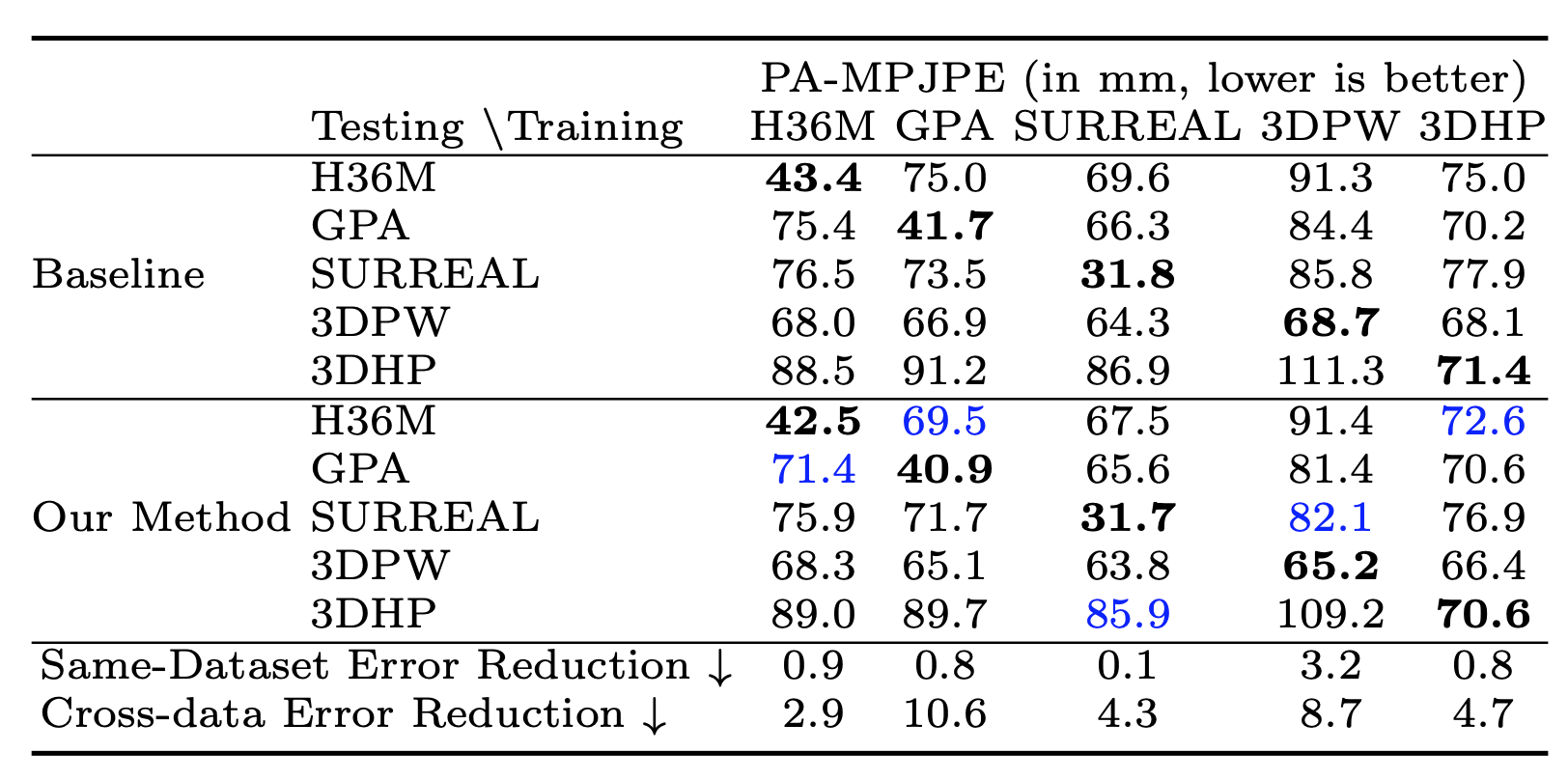
Baseline cross-dataset test error and error reduction (Procrustese aligned MPJPE) from the addition of our proposed quaternion loss. Bold indicates the best performing model on each the test sets (rows). Blue color indicates test set which saw greatest error reduction.
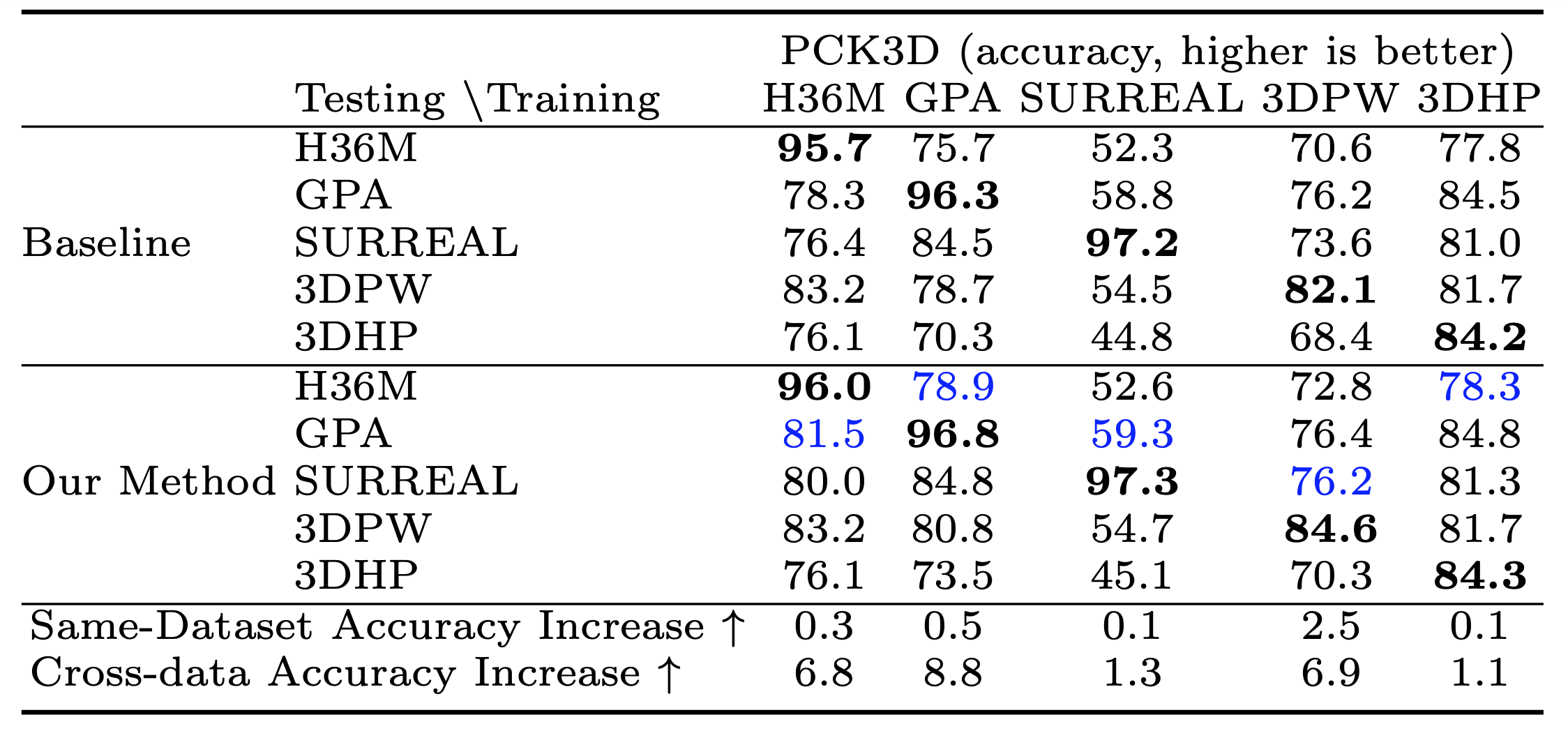
Baseline cross-dataset test accuracy and accuracy increases (PCK3D) from the addition of our proposed quaternion loss. Bold indicates the best performing model on each the test set (rows). Blue color indicates test set which saw greatest accuracy increase.
Retraining the model of Zhou et al. [50] using our viewpoint prediction loss also shows significant decrease in prediction error, demonstrating the generality of our finding.
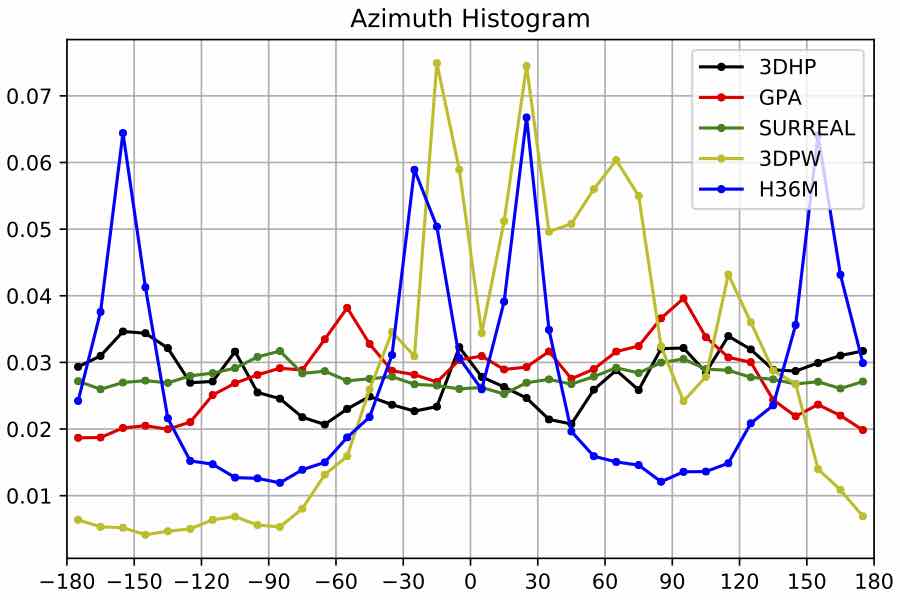
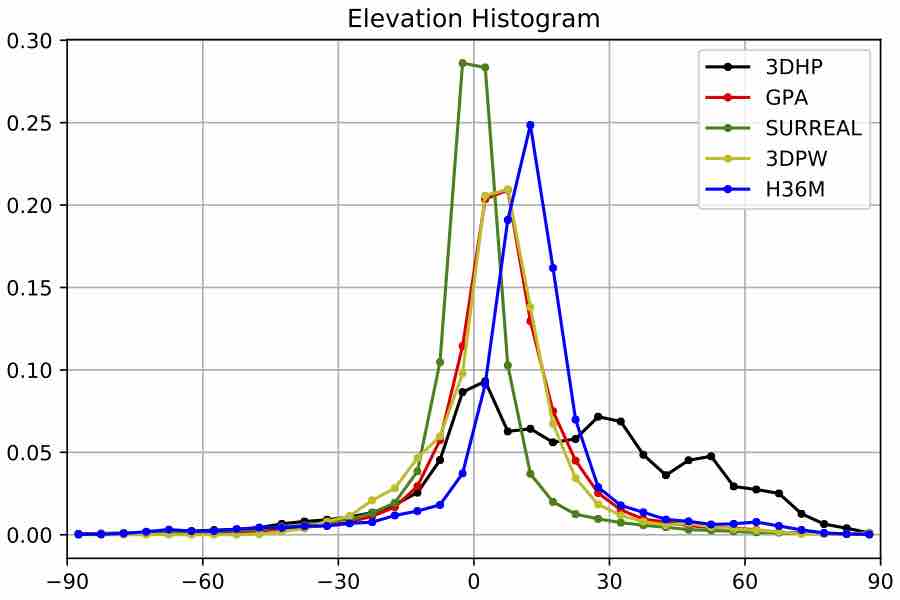
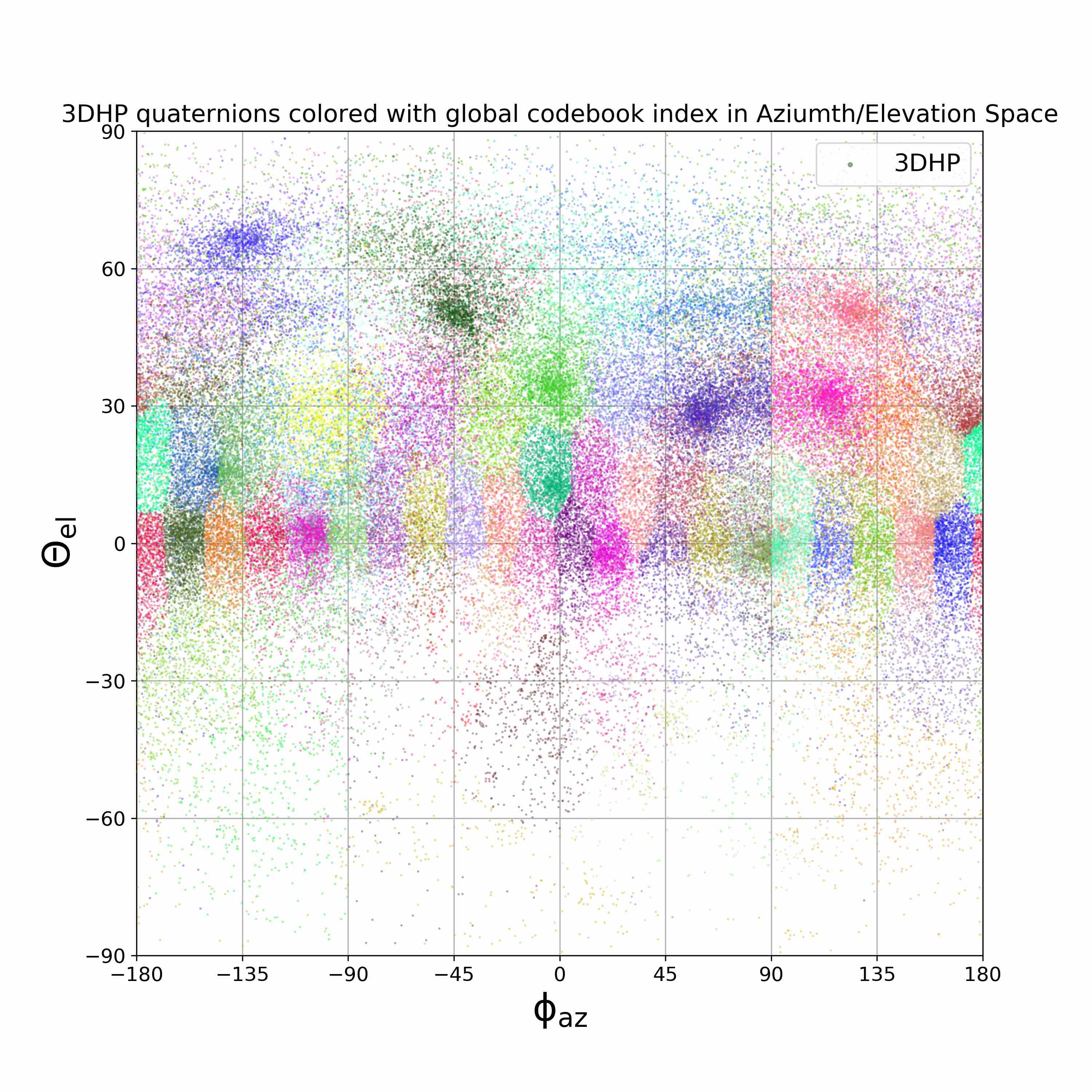
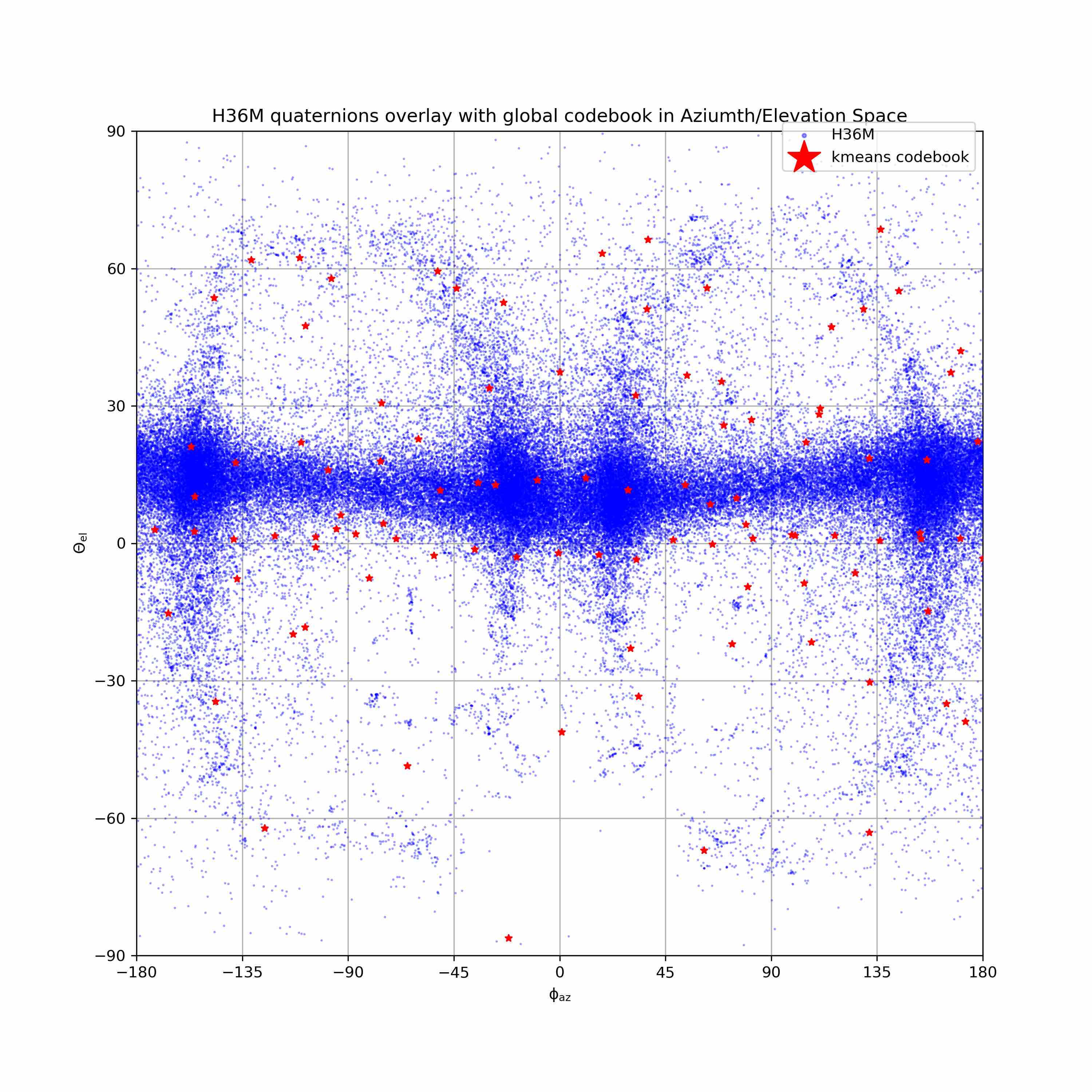
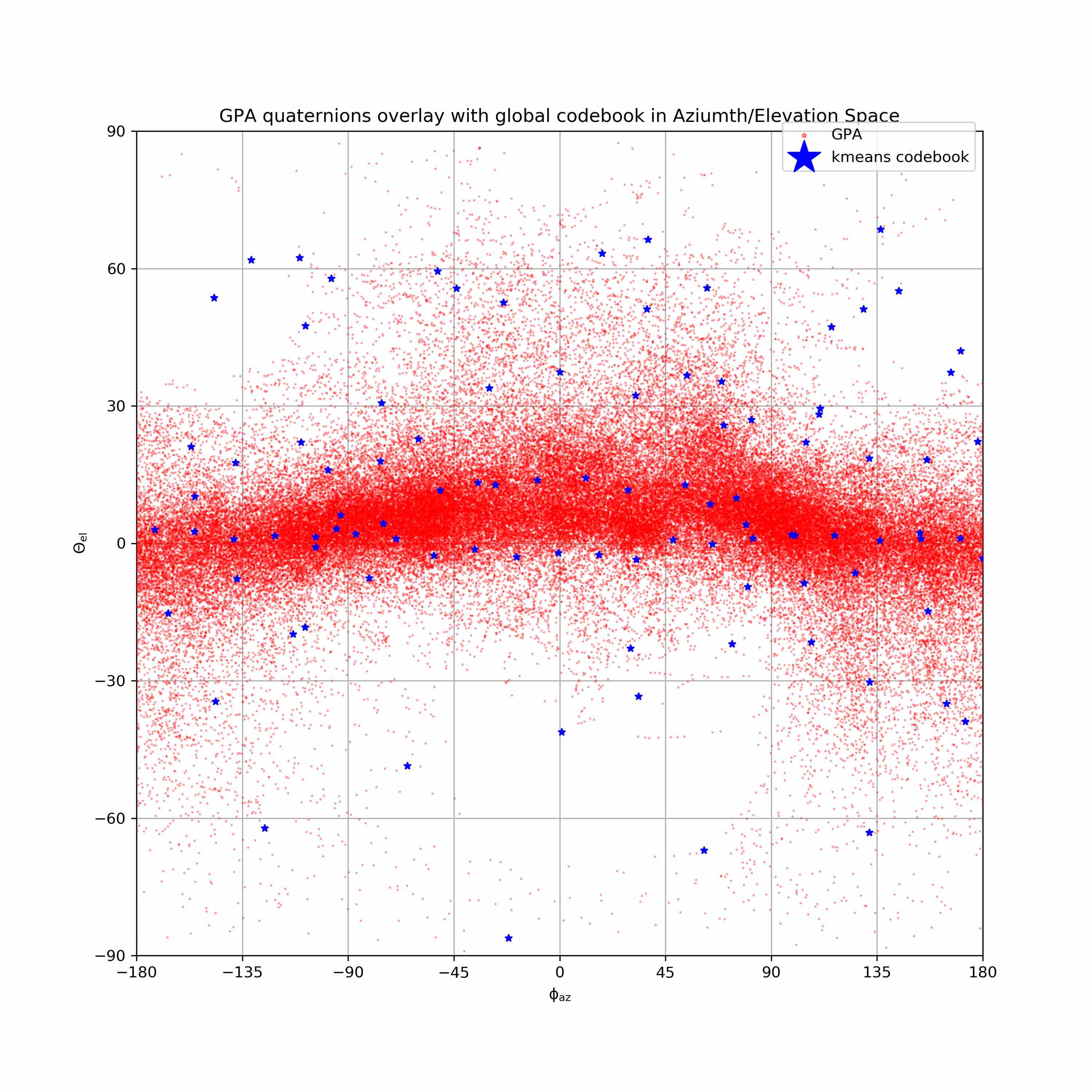
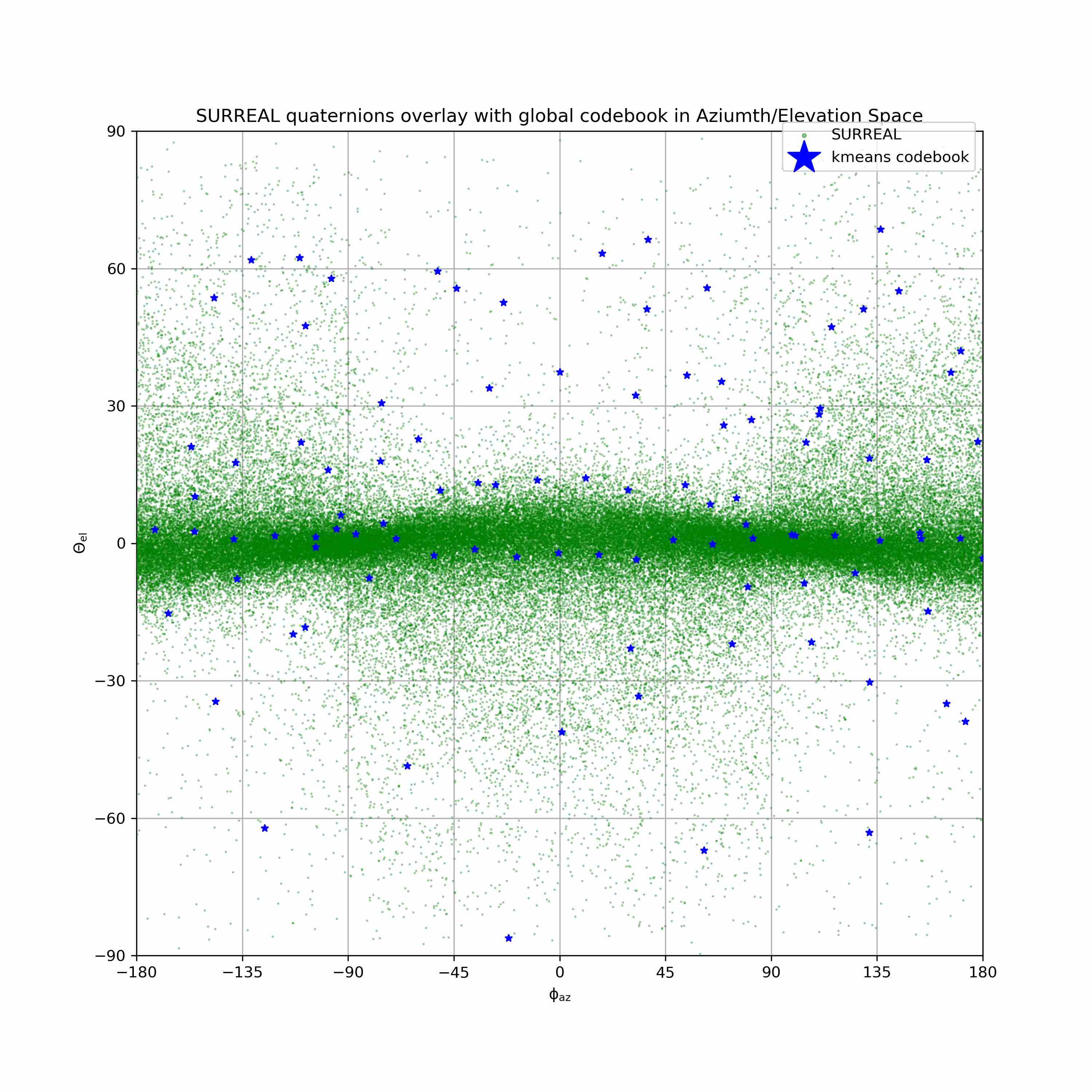
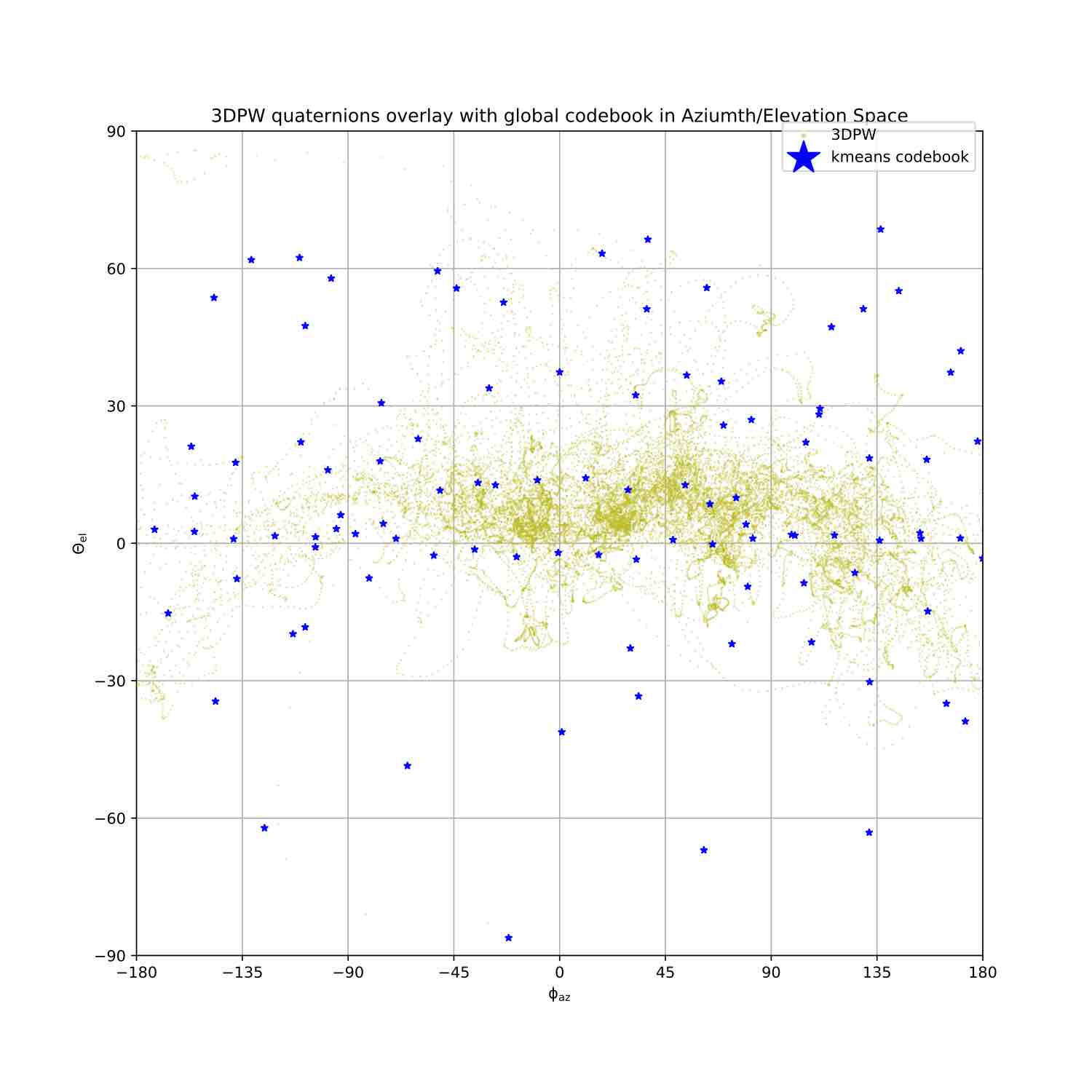
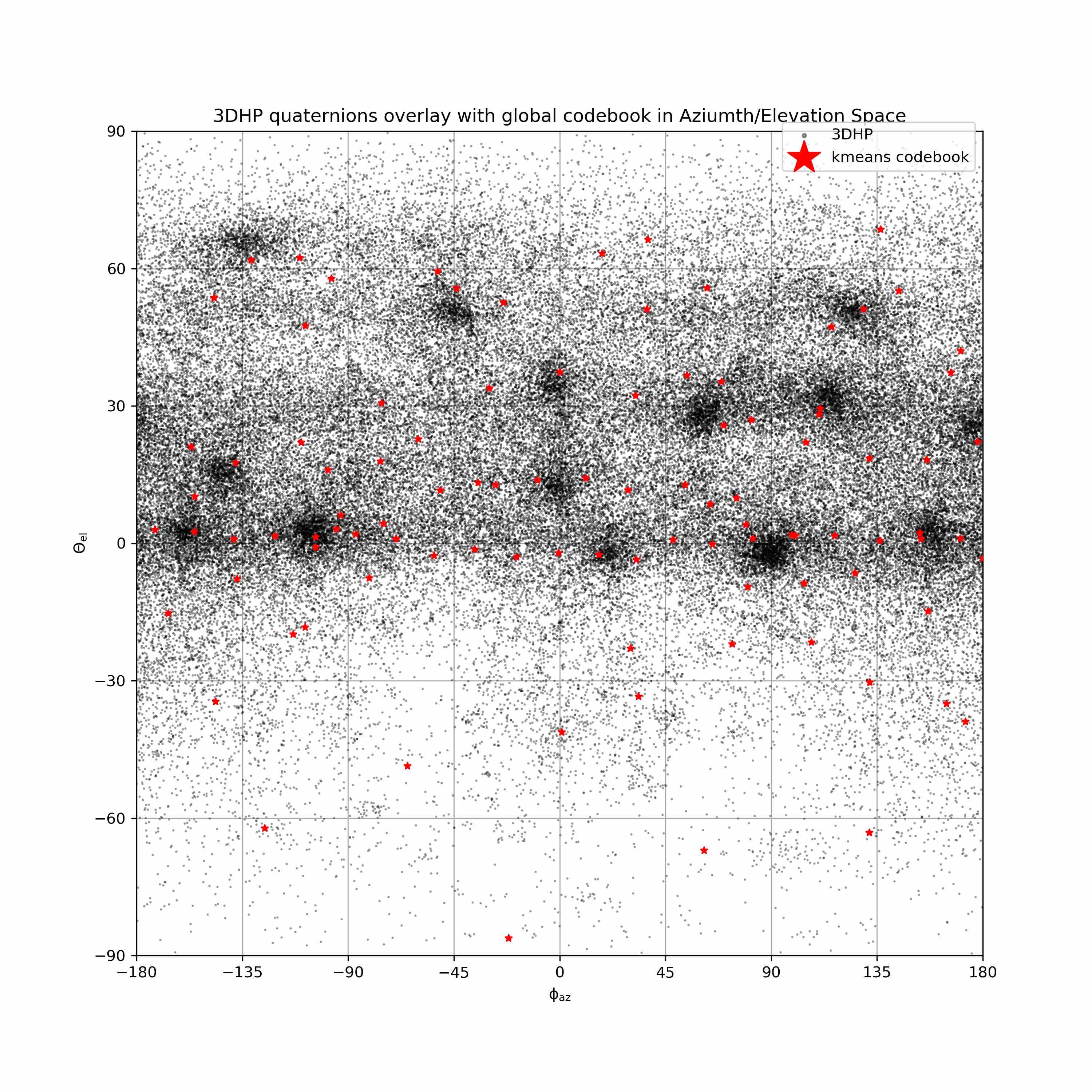
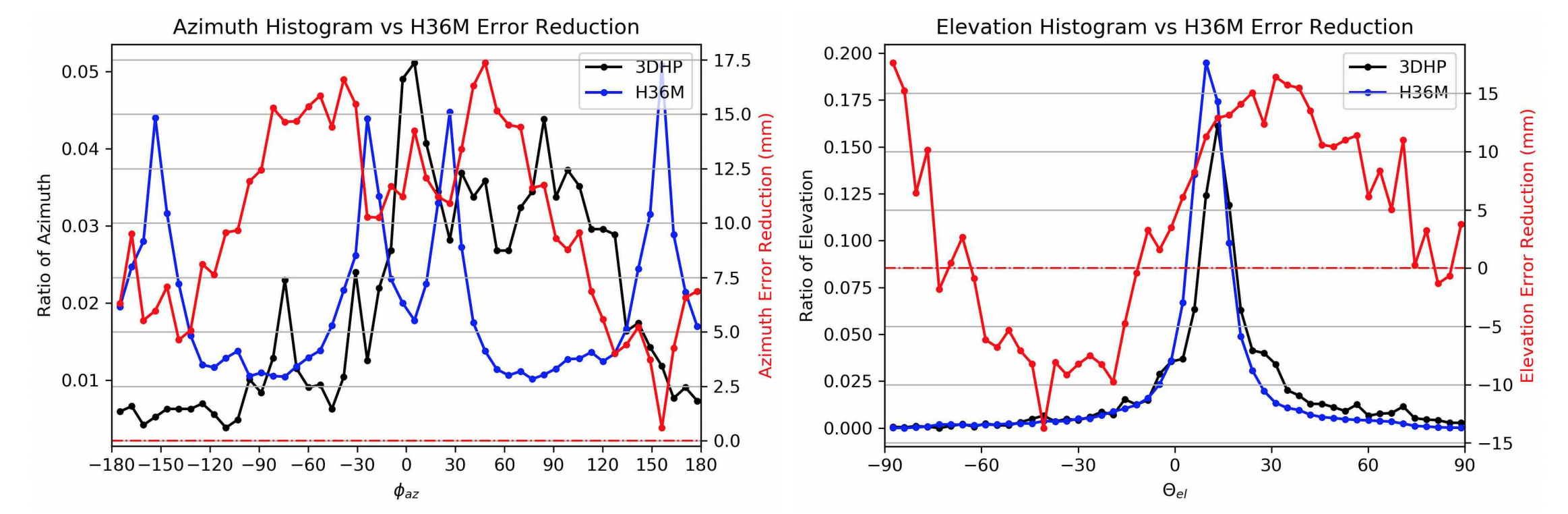
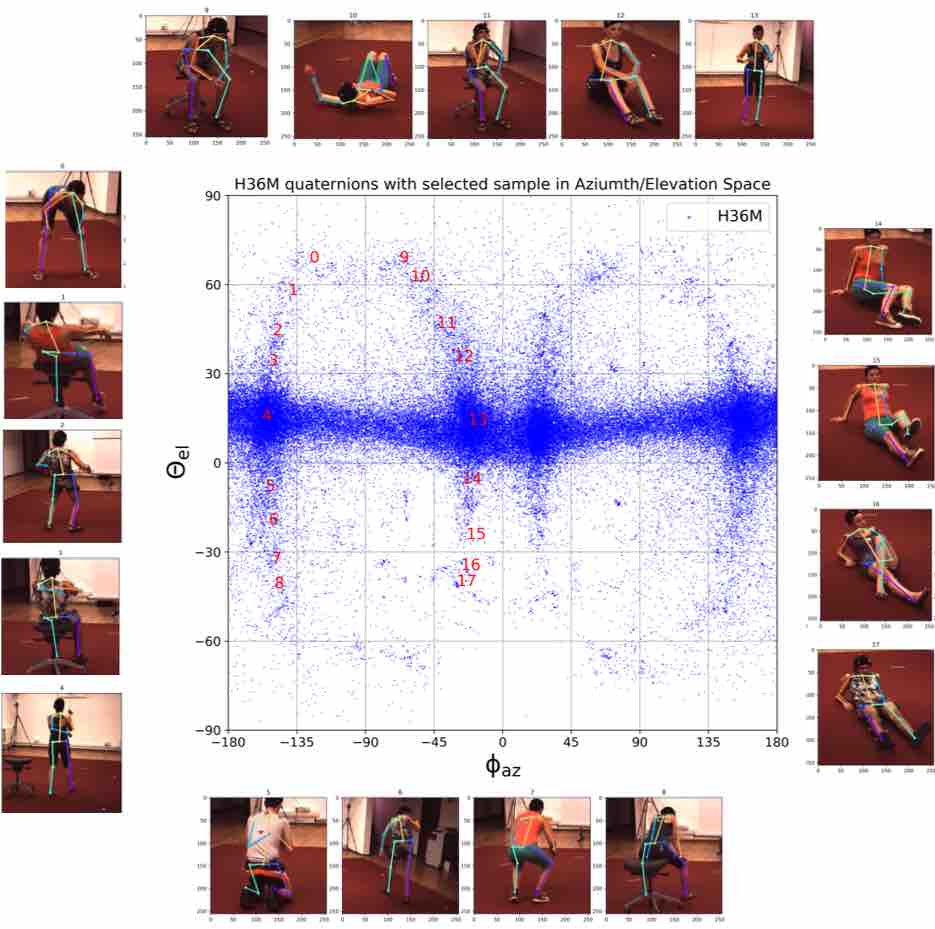
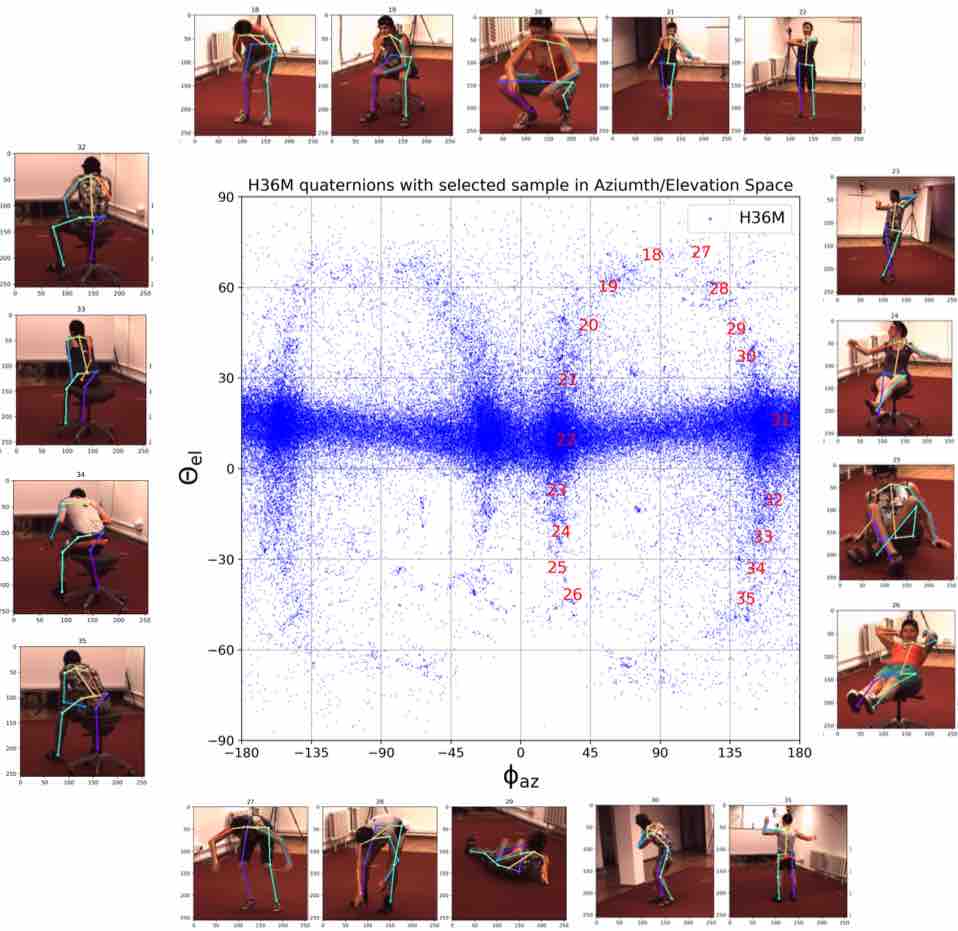
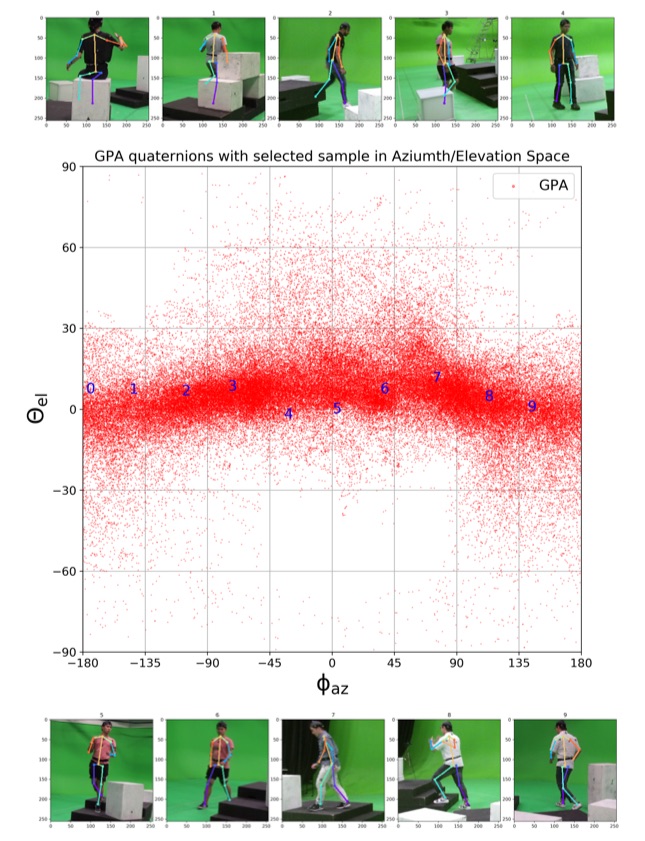
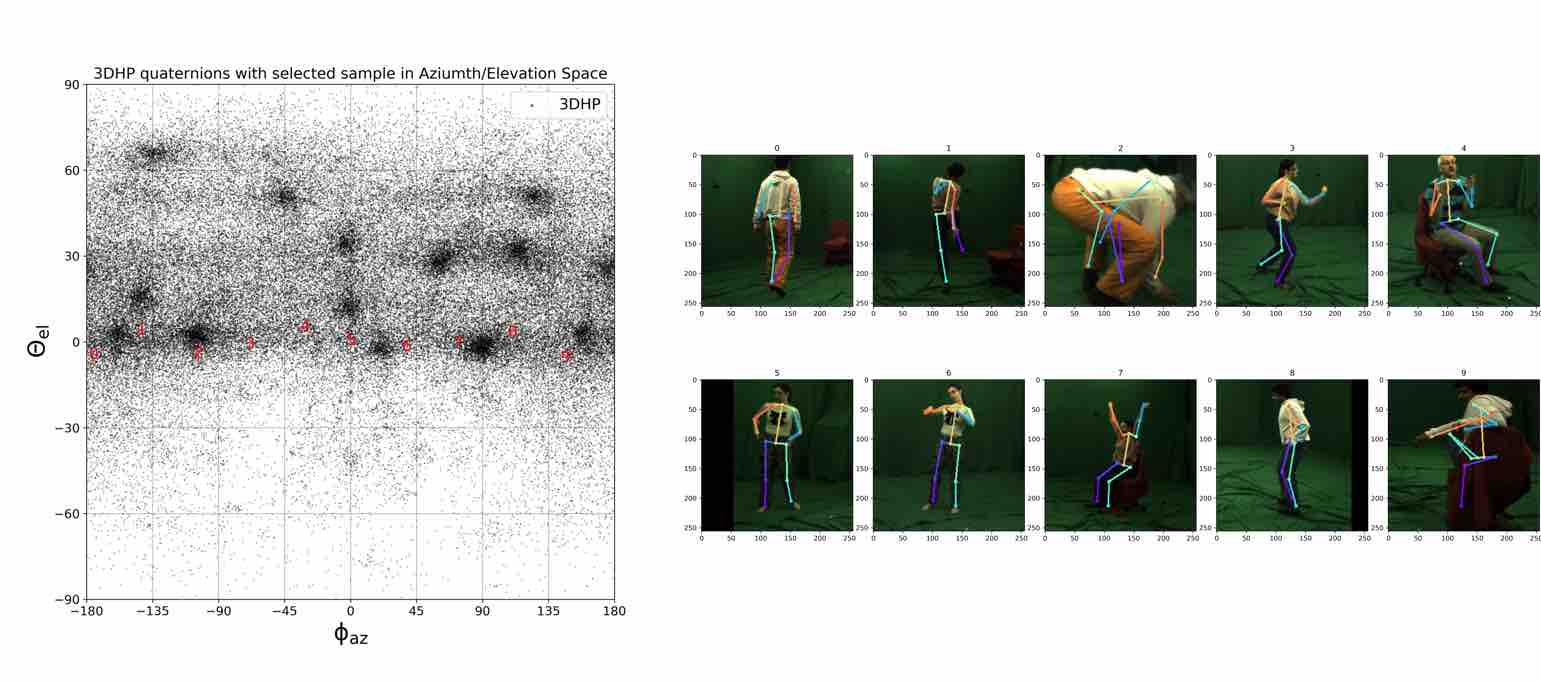
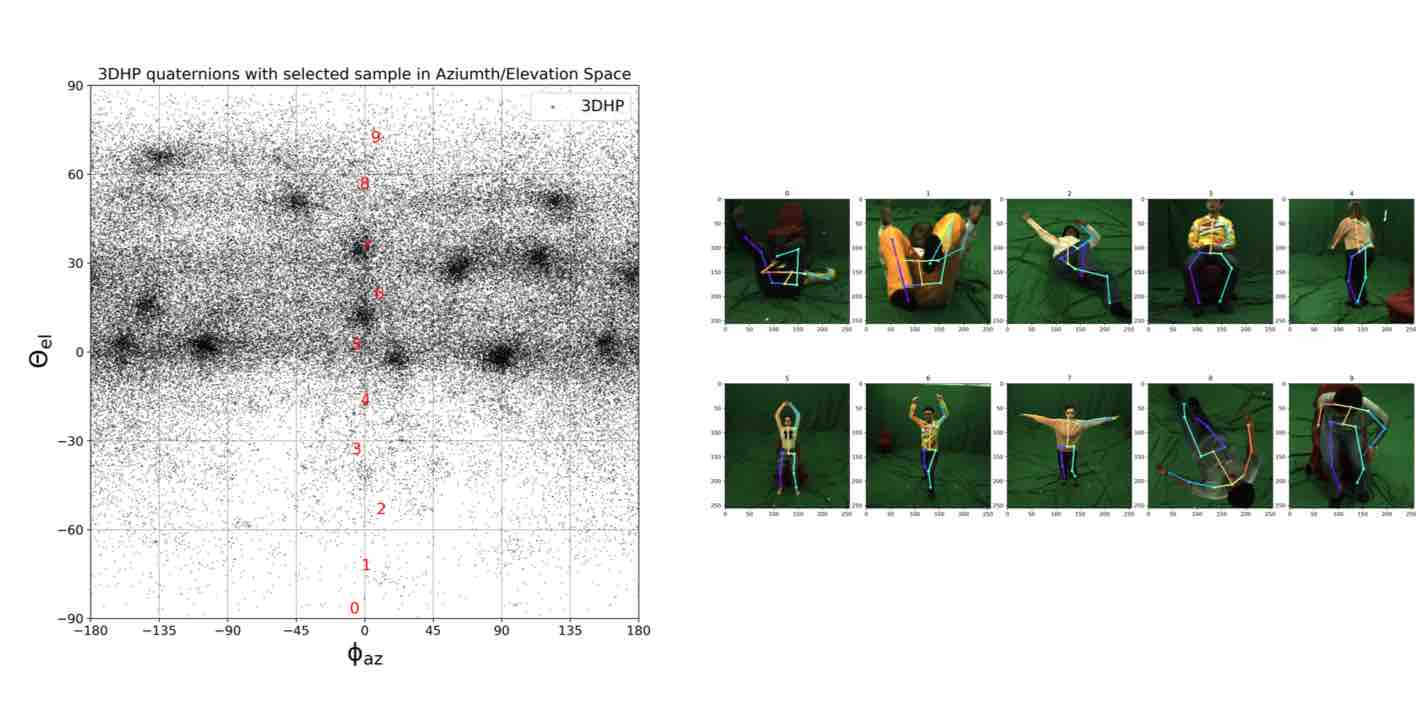
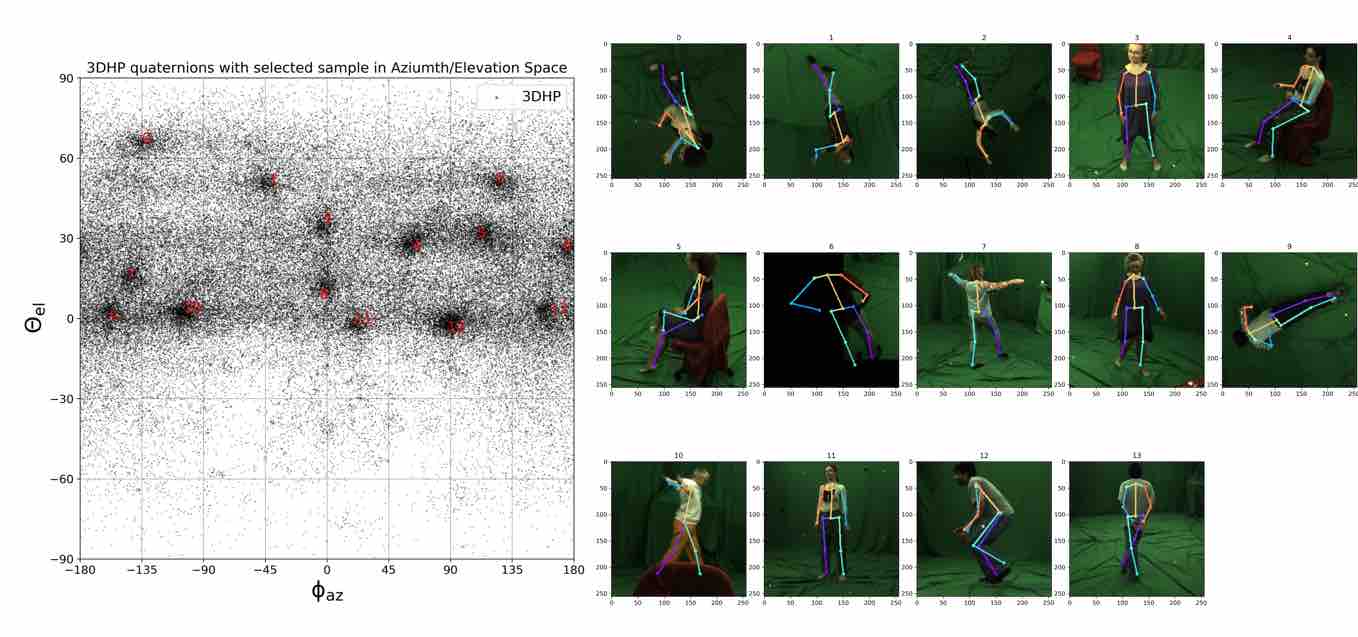
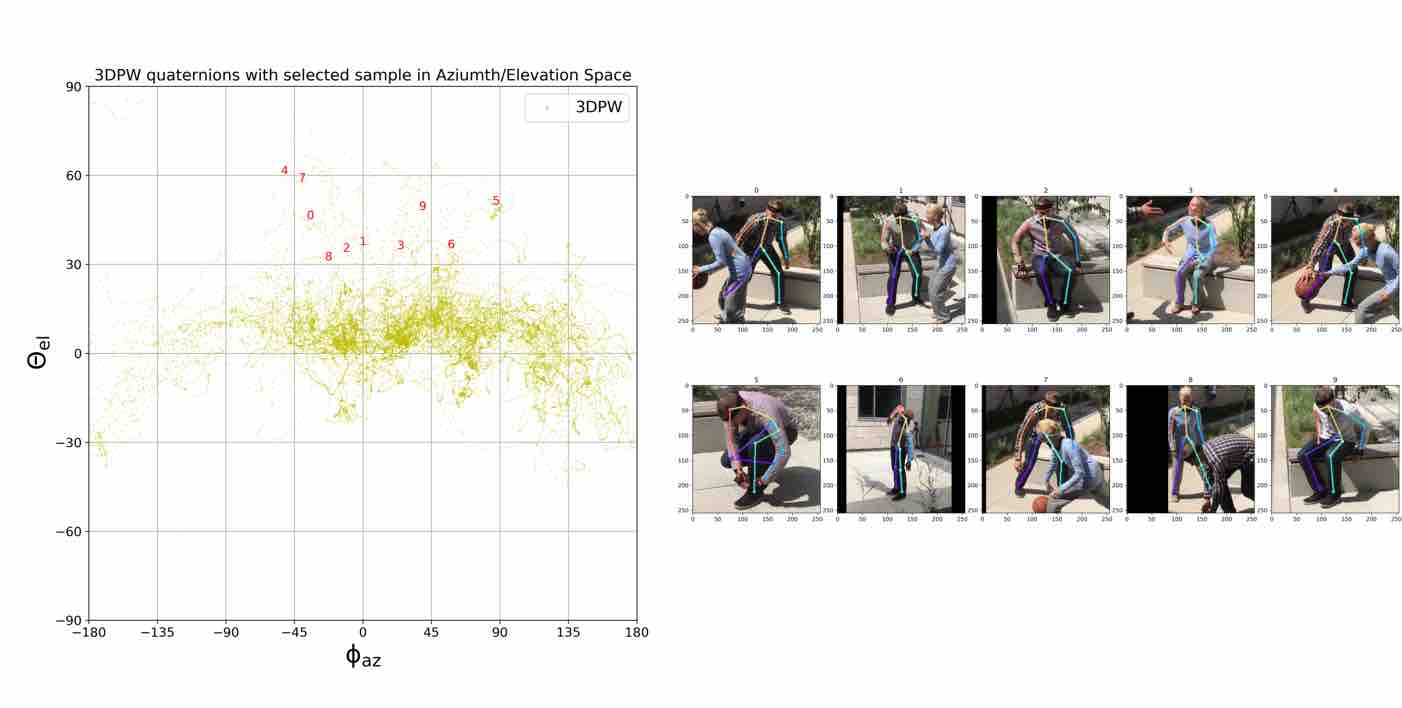
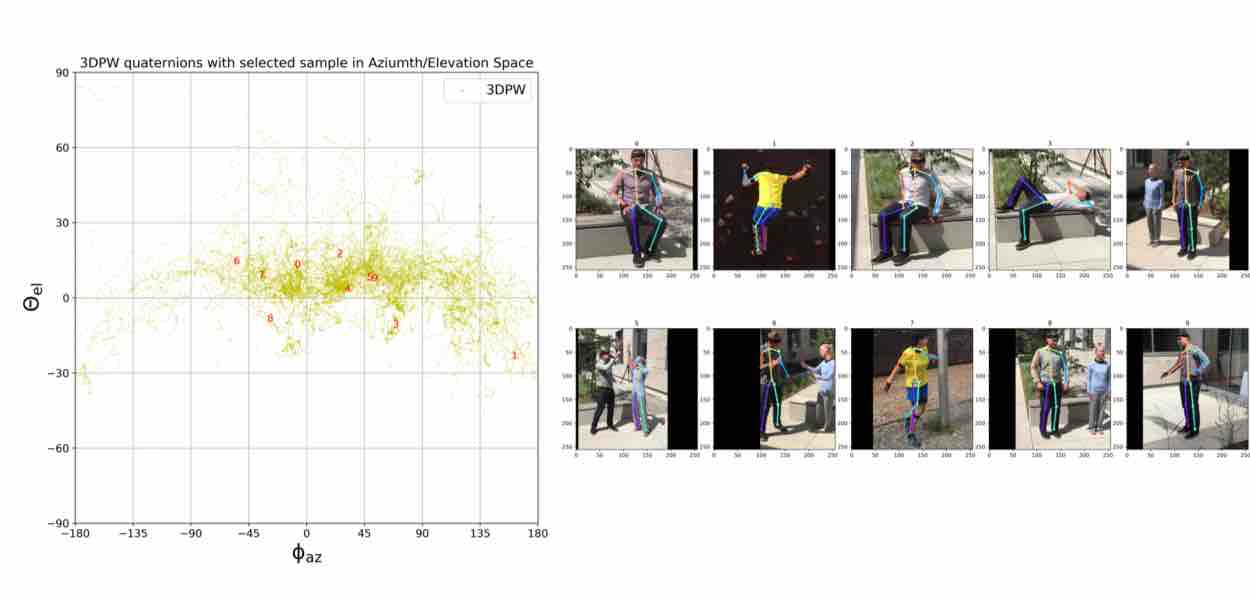
We visualize viewpoint distributions for train (3DHP) and test (H36M) overlayed with the reduction in pose prediction error relative to baseline

• Sampled images from H36M: We sample images from the interesting azimuth/elevation pattern from H36M. We can see the images from left are facing right while images from right are facing left. The index in the azimuth/elevation images corresponds with the index on top of images sampled and placed around the center figure

• Sampled images from GPA/SURREAL: We sample images from SURREAL and GPA with uniform azimuth from left to right, and place some randomness on elevation during sampling. We can see the patterns of sampled images from left to right: facing towards back and rotating to facing right, and facing towards the camera, and then facing back again.

• Sampled images from 3DHP, We sample images from 3DHP with uniform azimuth from left to right as shown in the first image, uniform elevation from top to down as shown in the third image, and from camera center. As shown in the third image, during sampling we add some randomness on sampled elevation/azimuth around camera centers.



• Sampled images from 3DPW: We sample images from 3DPW with extreme elevation as shown in the first image, and randomly as shown in the second image.

• Model predictions on 5 datasets from model trained on Human3.6M dataset. The 2d joints are overlaid with the original image, while the 3d prediction (red) is overlaid with 3d ground truth (blue). 3D prediction is visualized in body- centered coordinate rotated by the relative rotation between ground truth camera-centered coordinate and body-centered coordinate. From top to bottom are H36M, GPA, SURREAL, 3DPW and 3DHP datasets. We rank the images from left to right in order of increasing MPJPE.

• Trained on GPA and test on five datasets.

• Trained on SURREAL and test on five datasets.

• Trained on 3DPW and test on five datasets.

• Trained on 3DHP and test on five datasets.

• Model trained on 5 models tested on the same images from H36M, from left to right (model trained on H36M, GPA, SURREAL, 3DPW, 3DHP). The 2d joints are overlaid with the original image, while the 3d prediction (red) is overlaid with 3d ground truth (blue).

• Model trained on 5 models tested on the same images from GPA, from left to right (model trained on H36M, GPA, SURREAL, 3DPW, 3DHP).

• Model trained on 5 models tested on the same images from SURREAL, from left to right (model trained on H36M, GPA, SURREAL, 3DPW, 3DHP).

• Model trained on 5 models tested on the same images from 3DPW, from left to right (model trained on H36M, GPA, SURREAL, 3DPW, 3DHP).

• Model trained on 5 models tested on the same images from 3DHP, from left to right (model trained on H36M, GPA, SURREAL, 3DPW, 3DHP).